Etäisyys tulivuoreen
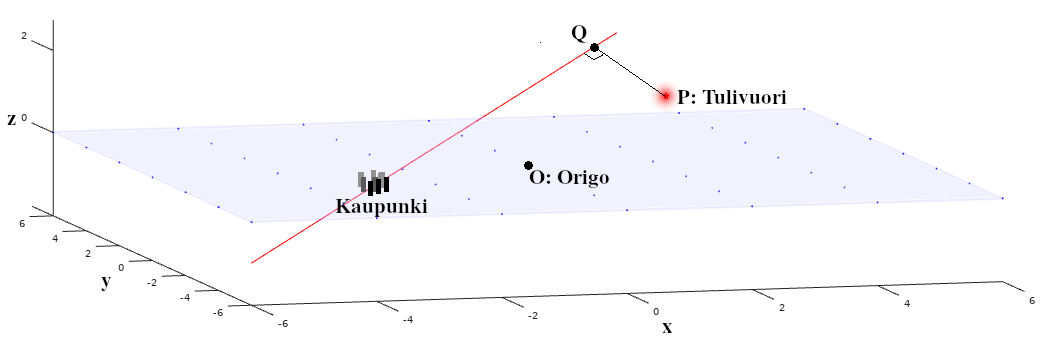
Katso yllä näkyvää kuvaa. Kuvassa näkyvät kaikki tämän tehtävän kannalta oleelliset elementit.
Idea on tämä: Pisteessä on kaupunki, ja siitä aiotaan rakentaa junatunneli kohti koillista (positiivisen x-akselin ja positiivisen y-akselin suuntaan). Tunnelin on tarkoitus lähteä kaupungista vektorin suuntaan. Matkassa on vain yksi pulma: suunnilleen samassa suunnassa on aktiiviseksi tunnettu tulivuori, pisteessä . Junatunneli ei saa kulkea 2 kilometriä lähempää tulivuorta, tai muuten hanketta ei voida turvallisuussyistä toteuttaa. Kysymys kuuluu, mikä on lyhin etäisyys suunnitellusta junatunnelista tulivuoreen? Mikä on se junatunnelin piste, joka olisi tulivuorta lähimpänä?
---------------------
Ratkaisu:
Kirjoitetaan sen suoran yhtälö, joka edustaa junatunnelia. Tunnemme pisteen, jonka kautta tunnelin kulkee (kaupunki), ja sen lisäksi tunnemme suoran suuntavektorin. Yleinen suoralla sijaitseva piste voidaan kirjoittaa
ja tässä merkinnässä tunnemme vektorit
ja
Kutsutaan tulivuorta pisteeksi P, ja kirjoitetaan
Suoralla (junatunnelilla) oleva piste voidaan kirjoittaa nyt
Vektori voidaan kirjoittaa
Tässä vaiheessa kannattaa varmistaa kuvasta, että olet ymmärtänyt mitkä vektorit muodostuvat mitenkin, ja miksi.
Nyt olemme lähellä ratkaisua. Tiedämme, että yleinen suoran piste Q on lähimpänä P:tä (vuorta) silloin, kun ja ovat toisiaan vastaan kohtisuorassa. Ratkaistaan pistetulosta, millä parametrin arvolla tämä tapahtuu.
Nyt kun tunnemme mikä :n arvo nimimoi junatunnelin ja tulivuoren etäisyyden, voimme laskea sen. Tämä etäisyys on toki vain vektorin pituus tällä :n arvolla.
Alussa sanottiin, että projektia ei voida jatkaa, jos tunneli menee 2 km lähempää tulivuorta. Saatu etäisyys on pienempi, joten projektia ei tälläisenään voida jatkaa.
Junatunnelin piste, joka on tulivuorta lähimpänä, löydetään, kun sijoitetaan :n arvo vektoriin , eli