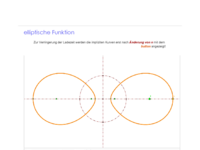
elliptische Funktion
Zur Verringerung der Ladezeit werden die impliziten Kurven erst nach Änderung von n mit dem button angezeigt!
Diese Seite ist Teil des GeoGebra-Books Moebiusebene. (August 2019) Kapitel: "Spezielle komplexe Funktionen"
Elliptische Funktionen sind komplex-differenzierbare Funktionen, welche einer Differential-Gleichung des Typs genügen- , wobei die Brennpunkte und die Scheitel festlegen. Nachtrag verbessert Februar 2020: in der 2. Klammer: statt
gebra?) die Kurven nicht mit einer explizit gegebenen komplexen Funktion anzeigen
wie zB. die zu oder gehörenden Kurven.
4 verschiedene Punkte auf einem Kreis besitzen stets 4 Symmetrie-Kreise (einer davon ist imaginär!).
Sie lassen sich mit Hilfe einer Möbius-Transformation so anordnen wie im Applet angezeigt.
Zu jeder Symmetrie gehören 2 Scheitelkreise; spiegelt man einen ausgewählten Brennpunkt (hier f), an diesen Scheitelkreisen, so erhält man Punkte der zugehörigen Leitkreise. Diese liegen in einem elliptischen Kreisbüschel
mit den Grundpunkten f und f#; f# erhält man als Spiegelbild von f an den Leitkreisen!
Fällt f# mit oder mit 1 zusammen, so ist die zugehörige Quartik Möbiustransformierte einer CASSINI-Quartik.
Gleichungen:
- Leitkreis zur y-Achsen-Symmetrie:
- Leitkreis zur Symmetrie am Einheitskreis:
- Leitkreis zur elliptischen Symmetrie:
- f#:
- f# = , dann ist und man erhält die CASSINI-Gleichung . Die CASSINI-Quartik kann man mit Wurzelfunktion "konstruieren"!
- f# = 1, dann ist und man erhält die Gleichung
