Ecuaciones de primer grado paso a paso
En esta página vamos a resolver ecuaciones de primer grado paso a paso. Comenzaremos con ecuaciones muy simples e iremos aumentando su dificultad.
Resolver una ecuación consiste en encontrar el valor que debe tomar la incógnita x para que se cumpla la igualdad. Podemos comprobar si la solución encontrada es correcta sustituyendo la incógnita x por la solución.
Ecuación 1
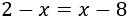 Para resolver la ecuación, debemos pasar los monomios que tienen la incógnita a una lado de la igualdad y los que no tienen la incógnita al otro lado.
Como 8 está restando en la derecha, pasa sumando al lado izquierdo:
Para resolver la ecuación, debemos pasar los monomios que tienen la incógnita a una lado de la igualdad y los que no tienen la incógnita al otro lado.
Como 8 está restando en la derecha, pasa sumando al lado izquierdo:
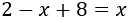 Como x está restando en la izquierda, pasa restando a la derecha:
Como x está restando en la izquierda, pasa restando a la derecha:
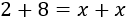 Ahora que ya tenemos separados los monomios con y sin la incógnita, podemos sumarlos. En la izquierda, sumamos 2+8 y, en la derecha, x+x:
Ahora que ya tenemos separados los monomios con y sin la incógnita, podemos sumarlos. En la izquierda, sumamos 2+8 y, en la derecha, x+x:
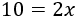 Para ver con claridad el paso siguiente, escribimos 2x como un producto:
Para ver con claridad el paso siguiente, escribimos 2x como un producto:
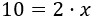 Para terminar, debemos pasar el coeficiente de la incógnita (el número 2 que multiplica a x) al lado izquierdo. Como el número 2 está multiplicando, pasa dividiendo:
Para terminar, debemos pasar el coeficiente de la incógnita (el número 2 que multiplica a x) al lado izquierdo. Como el número 2 está multiplicando, pasa dividiendo:
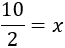 Simplificando la fracción,
Simplificando la fracción,
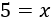 Por tanto, la solución de la ecuación es x=5. Para comprobar la solución, sustituimos x por 5 en la ecuación:
Por tanto, la solución de la ecuación es x=5. Para comprobar la solución, sustituimos x por 5 en la ecuación:
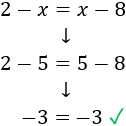 Como hemos obtenido una igualdad verdadera (-3 es igual a -3), la solución es correcta. Si, por el contrario obtenemos una igualdad falsa, significa que hemos cometido algún error en la resolución de la ecuación.
Como hemos obtenido una igualdad verdadera (-3 es igual a -3), la solución es correcta. Si, por el contrario obtenemos una igualdad falsa, significa que hemos cometido algún error en la resolución de la ecuación.
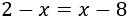 Para resolver la ecuación, debemos pasar los monomios que tienen la incógnita a una lado de la igualdad y los que no tienen la incógnita al otro lado.
Como 8 está restando en la derecha, pasa sumando al lado izquierdo:
Para resolver la ecuación, debemos pasar los monomios que tienen la incógnita a una lado de la igualdad y los que no tienen la incógnita al otro lado.
Como 8 está restando en la derecha, pasa sumando al lado izquierdo:
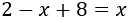 Como x está restando en la izquierda, pasa restando a la derecha:
Como x está restando en la izquierda, pasa restando a la derecha:
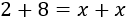 Ahora que ya tenemos separados los monomios con y sin la incógnita, podemos sumarlos. En la izquierda, sumamos 2+8 y, en la derecha, x+x:
Ahora que ya tenemos separados los monomios con y sin la incógnita, podemos sumarlos. En la izquierda, sumamos 2+8 y, en la derecha, x+x:
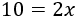 Para ver con claridad el paso siguiente, escribimos 2x como un producto:
Para ver con claridad el paso siguiente, escribimos 2x como un producto:
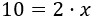 Para terminar, debemos pasar el coeficiente de la incógnita (el número 2 que multiplica a x) al lado izquierdo. Como el número 2 está multiplicando, pasa dividiendo:
Para terminar, debemos pasar el coeficiente de la incógnita (el número 2 que multiplica a x) al lado izquierdo. Como el número 2 está multiplicando, pasa dividiendo:
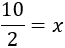 Simplificando la fracción,
Simplificando la fracción,
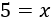 Por tanto, la solución de la ecuación es x=5. Para comprobar la solución, sustituimos x por 5 en la ecuación:
Por tanto, la solución de la ecuación es x=5. Para comprobar la solución, sustituimos x por 5 en la ecuación:
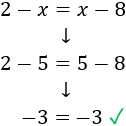 Como hemos obtenido una igualdad verdadera (-3 es igual a -3), la solución es correcta. Si, por el contrario obtenemos una igualdad falsa, significa que hemos cometido algún error en la resolución de la ecuación.
Como hemos obtenido una igualdad verdadera (-3 es igual a -3), la solución es correcta. Si, por el contrario obtenemos una igualdad falsa, significa que hemos cometido algún error en la resolución de la ecuación.Ecuación 2
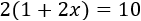 En esta ecuación tenemos un paréntesis. Un paréntesis sirve para representar que una misma operación se aplica a un grupo de monomios. El número que está delante del paréntesis está multiplicándolo, así que podemos escribir la ecuación como
En esta ecuación tenemos un paréntesis. Un paréntesis sirve para representar que una misma operación se aplica a un grupo de monomios. El número que está delante del paréntesis está multiplicándolo, así que podemos escribir la ecuación como
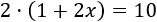 En la ecuación, el paréntesis nos dice que debemos multiplicar los monomios 1 y 2x por 2. Por tanto, podemos eliminar el paréntesis escribiendo su significado:
En la ecuación, el paréntesis nos dice que debemos multiplicar los monomios 1 y 2x por 2. Por tanto, podemos eliminar el paréntesis escribiendo su significado:
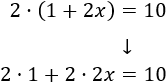 Calculamos los productos:
Calculamos los productos:
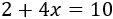 Finalmente, resolvemos la ecuación anterior:
Finalmente, resolvemos la ecuación anterior:
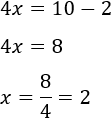 Por tanto, la solución de la ecuación es x=2.
Por tanto, la solución de la ecuación es x=2.
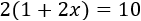 En esta ecuación tenemos un paréntesis. Un paréntesis sirve para representar que una misma operación se aplica a un grupo de monomios. El número que está delante del paréntesis está multiplicándolo, así que podemos escribir la ecuación como
En esta ecuación tenemos un paréntesis. Un paréntesis sirve para representar que una misma operación se aplica a un grupo de monomios. El número que está delante del paréntesis está multiplicándolo, así que podemos escribir la ecuación como
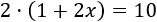 En la ecuación, el paréntesis nos dice que debemos multiplicar los monomios 1 y 2x por 2. Por tanto, podemos eliminar el paréntesis escribiendo su significado:
En la ecuación, el paréntesis nos dice que debemos multiplicar los monomios 1 y 2x por 2. Por tanto, podemos eliminar el paréntesis escribiendo su significado:
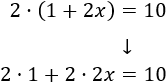 Calculamos los productos:
Calculamos los productos:
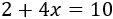 Finalmente, resolvemos la ecuación anterior:
Finalmente, resolvemos la ecuación anterior:
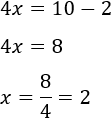 Por tanto, la solución de la ecuación es x=2.
Por tanto, la solución de la ecuación es x=2.Ecuación 3
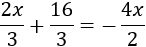 Si multiplicamos por 3 la ecuación, desaparecen las fracciones cuyo denominador es 3. Pero quedará la fracción cuyo denominador es 2. Para eliminar los denominadores de un solo paso, multiplicamos la ecuación por el mínimo común múltiplo de los denominadores.
El mínimo común múltiplo de 2 y 3 es 6. Por tanto, multiplicamos por 6 la ecuación:
Si multiplicamos por 3 la ecuación, desaparecen las fracciones cuyo denominador es 3. Pero quedará la fracción cuyo denominador es 2. Para eliminar los denominadores de un solo paso, multiplicamos la ecuación por el mínimo común múltiplo de los denominadores.
El mínimo común múltiplo de 2 y 3 es 6. Por tanto, multiplicamos por 6 la ecuación:
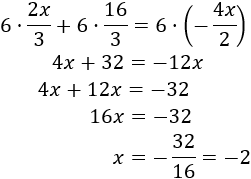
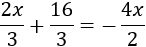 Si multiplicamos por 3 la ecuación, desaparecen las fracciones cuyo denominador es 3. Pero quedará la fracción cuyo denominador es 2. Para eliminar los denominadores de un solo paso, multiplicamos la ecuación por el mínimo común múltiplo de los denominadores.
El mínimo común múltiplo de 2 y 3 es 6. Por tanto, multiplicamos por 6 la ecuación:
Si multiplicamos por 3 la ecuación, desaparecen las fracciones cuyo denominador es 3. Pero quedará la fracción cuyo denominador es 2. Para eliminar los denominadores de un solo paso, multiplicamos la ecuación por el mínimo común múltiplo de los denominadores.
El mínimo común múltiplo de 2 y 3 es 6. Por tanto, multiplicamos por 6 la ecuación:
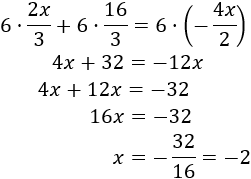
Más ecuaciones resueltas:
- Ecuaciones de primer grado paso a paso
- Teorema de Pitágoras: problemas
- Potencias: propiedades y ejemplos
- Fracciones equivalentes y fracción irreductible
- Ecuaciones de primer grado: problemas
- Sistemas de ecuaciones (métodos)
- Sistemas de ecuaciones lineales: problemas
- Ecuaciones de segundo grado paso a paso
- Problemas de mcm y MCD
- Problemas de MRU
- Integración por partes
- Introducción a las progresiones: aritméticas y geométricas
- Ecuaciones exponenciales explicadas
- Problemas y Ecuaciones .com