Criterio generale di parallelismo
La congruenza di una coppia di angoli alterni interni equivale:
- alla congruenza di una coppia di angoli alterni esterni
- alla congruenza di una coppia di angoli corrispondenti
- alla condizione che una coppia di angoli coniugati siano supplementari
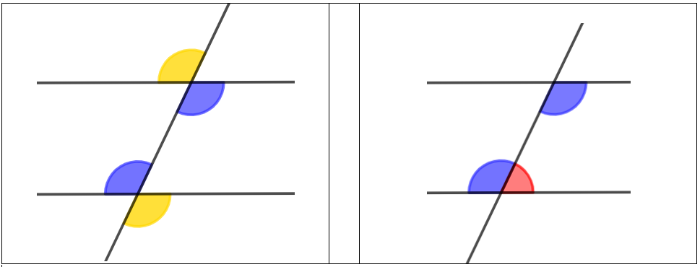
Dimostrazione
- Gli angoli alterni interni sono congruenti se e solo se sono congruenti gli angoli alterni esterni perchè ciascuno degli angoli alterni esterni è congruente a uno degli angoli alterni interni perchè sono opposti al vertice.
- Gli angoli alterni interni sono congruenti se e solo se sono congruenti gli angoli corrispondenti perchè l'angolo "giallo" è congruente a uno degli angoli alterni interni (blu) perchè sono opposti al vertice.
- Se due angoli alterni interni sono congruenti, allora l'angolo "rosso" deve essere supplementare dell'angolo "blu" perchè sono adiacenti; quindi, i due angoli coniugati (uno rosso e uno blu) sono supplementari. Viceversa, se due angoli coniugati (uno rosso e uno blu) sono supplementari, allora i due angoli alterni interni (blu) devono essere congruenti perchè sono supplementari dello stesso angolo (rosso).
Teorema
Due rette, tagliate da una trasversale, sono parallele se e solo se:
- formano una coppia di angoli alterni interni congruenti
- formano una coppia di angoli alterni esterni congruenti
- formano una coppia di angoli corrispondenti congruenti
- formano una coppia di angoli coniugati supplementari