Εξισώσεις Ά -1ου βαθμού
Εξισώσεις
Μεταβλητή
λέγεται κάθε αριθμός που μεταβάλλεται, δηλαδή κάθε αριθμός που μπορεί να πάρει πολλές τιμές.
Συμβολίζεται με ένα μικρό γράμμα του ελληνικού ή του λατινικού αλφάβητου (x, y, α, β).
Εξίσωση
λέγεται κάθε ισότητα που έχει έναν άγνωστο (μεταβλητή), αριθμούς και πράξεις μεταξύ τους.
Για παράδειγμα, μια εξίσωση είναι η 3x + 200 = x + 600.
Η παράσταση 3x + 200 λέγεται πρώτο μέλος της εξίσωσης, ενώ
η παράσταση x + 600 λέγεται δεύτερο μέλος αυτής.
Λύση ή ρίζα
της εξίσωσης είναι ο αριθμός που επαληθεύει την εξίσωση.
πχ η λύση της εξίσωσης x+3=9 είναι η x=6, αφού 6+3=9.
Η διαδικασία που κάνουμε για να φτάσουμε στη λύση της εξίσωσης λέγεται επίλυση της εξίσωσης.
Εξισώσεις α βαθμού λέγονται οι εξισώσεις που έχουν μεγαλύτερη δύναμη της μεταβλητής την 1η.
Για παράδειγμα, εξίσωση α βαθμού (πρώτου βαθμού) είναι η 2x+1=9.
Ωστόσο, υπάρχουν εξισώσεις με βαθμό μεγαλύτερο από 1 ανάλογα με τη μεγαλύτερη δύναμη στην οποία εμφανίζεται η μεταβλητή. Για παράδειγμα,
η εξίσωση x2=4 είναι β βαθμού (δευτέρου βαθμού), ενώ
η εξίσωση x3=27 είναι γ βαθμού (τρίτου βαθμού).
Ιδιότητες ισότητας
Μια σχέση ισότητας είναι στην ουσία μια ζυγαριά, η οποία ισορροπεί.
Γενικότεροι κανόνες για τις ισότητες:
Αν και στα δύο μέλη μιας ισότητας προσθέσουμε τον ίδιο αριθμό, τότε προκύπτει και πάλι μια ισότητα.
Δηλαδή: Αν α = β τότε α + γ = β + γ
Αν και στα δύο μέλη μιας ισότητας αφαιρέσουμε τον ίδιο αριθμό, τότε προκύπτει και πάλι μια ισότητα.
Δηλαδή: Αν α = β τότε α - γ = β - γ
Αν και τα δύο μέλη μιας ισότητας πολλαπλασιαστούν με τον ίδιο αριθμό, τότε προκύπτει και πάλι μια ισότητα.
Δηλαδή: Αν α = β τότε α · γ = β · γ
Αν και τα δύο μέλη μιας ισότητας διαιρεθούν με τον ίδιο (μη μηδενικό) αριθμό, τότε προκύπτει και πάλι μια ισότητα.
Δηλαδή: Αν α = β τότε α:γ = β:γ , με γ ≠ 0 Γιατί πρέπει να βάλουμε τον περιορισμό γ ≠ 0 ;
Μια εξίσωση 1ου βαθμού έχει μοναδική λύση, ή είναι αόριστη ή είναι αδύνατη.
πχ1 η εξίσωση 2·x = 8 έχει μοναδική λύση x = 4
πχ2 η εξίσωση 0·x = 0 έχει άπειρες λύσεις δηλαδή είναι ταυτότητα ή αόριστη
πχ3 η εξίσωση 0·x = 5 δεν έχει καμία λύση δηλαδή είναι αδύνατη
Έστω η εξίσωση 3x + 200 = x + 600
Για να βρούμε τον άγνωστο x εργαζόμαστε ως εξής:
3x + 200 = x + 600
Αφαιρούμε το 200 και από τα δύο μέλη της εξίσωσης
3x + 200 – 200 = x + 600 – 200
Κάνουμε τις πράξεις
3x = x + 400
Αφαιρούμε το x και από τα δύο μέλη της εξίσωσης
3x – x = x + 400 – x
Κάνουμε αναγωγή ομοίων όρων και πράξεις
(3 – 1)x = 400
άρα 2x = 400
Διαιρούμε με το 2 και τα δύο μέλη της εξίσωσης
Απλοποιούμε τα κλάσματα και έχουμε τη
λύση - ρίζα: x = 200
Όταν λύνουμε μια εξίσωση για να είμαστε σίγουροι ότι το έχουμε επιλύσει σωστά, στο τέλος κάνουμε επαλήθευση. Στο πρόβλημά μας
για x = 200 έχουμε:
Πρώτο μέλος: 3 ∙ 200 + 200 = 600 + 200 = 800
Δεύτερο μέλος: 200 + 600 = 800
Άρα η τιμή που βρήκαμε είναι σωστή!
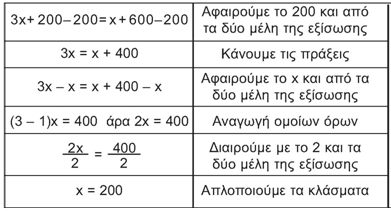
Στην παραπάνω λύση της εξίσωσης 3x + 200 = x + 600 «απομονώσαμε» το x στο πρώτο μέλος
της εξίσωσης, προσθέτοντας ή αφαιρώντας και στα δύο μέλη τον ίδιο αριθμό.