Factorising quadratics, sketching and inequalities
Keywords
| English | Japanese | Korean | Chinese Simplified |
| Factorise/Factorize | 因数分解 | 인수분해 | 因式分解 |
| Quadratic Equation | 二次方程式 | 이차방정식 | 二次方程 |
| Roots | 根 | 근 | 根 |
| X-axis Intersection | X軸との交点 | x축과의 교점 | 与x轴的交点 |
| Graph Sketching | グラフのスケッチ | 그래프 스케치 | 绘图 |
| Discriminant | 判別式 | 판별식 | 判别式 |
| Leading Coefficient | 最高次係数 | 선도계수 | 首项系数 |
| Orientation of Quadratic Graph | 二次関数のグラフの向き | 이차함수 그래프의 방향 | 二次图形的方向 |
| Completing the Square | 平方完成 | 완전제곱식 | 配方法 |
| Quadratic Formula | 二次方程式の解の公式 | 이차방정식의 해 공식 | 二次方程的求根公式 |
| Solution Regions | 解の領域 | 해의 영역 | 解的区域 |
| Quadratic Inequalities | 二次不等式 | 이차부등식 | 二次不等式 |
| Factored Form | 因数分解された形 | 인수분해된 형태 | 因式分解形式 |
| Perfect Square | 完全平方 | 완전제곱 | 完全平方 |
| Critical Values | 臨界値 | 임계값 | 临界值 |
| Factual Questions | Conceptual Questions | Debatable Questions |
| 1. How do you factorise a quadratic equation in the form ? | 1. Explain the significance of the discriminant in solving quadratic equations. | 1. Is factoring always the most efficient method for solving quadratic equations? Why or why not? |
| 2. What are the roots of the quadratic equation ? | 2. Discuss how the sign of the leading coefficient affects the orientation of a quadratic graph. | 2. Debate the importance of learning to sketch quadratic graphs by hand in the age of graphing calculators. |
| 3. How do you determine if a quadratic graph will touch or intersect the x-axis? | 3. How does factoring a quadratic equation help in sketching its graph? | 3. Can understanding inequalities and their graphical representations enhance problem-solving skills in real-life situations? |
| 4. Sketch the graph of | 4. Compare and contrast the methods of solving quadratic equations: factoring, completing the square, and using the quadratic formula. | 4. Discuss the statement: "The ability to solve quadratic equations is more crucial than understanding their graphical implications." |
| 5. What is the solution to the inequality? | 5. Explain the concept of "solution regions" in quadratic inequalities. | 5. Evaluate the role of quadratic equations and their applications in higher mathematics and other disciplines. |
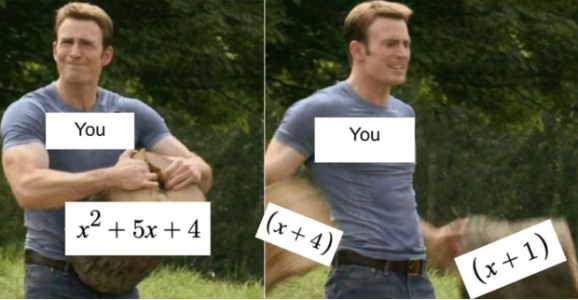
Mini-Investigation: The Quest for Quadratic Mastery
Explain a method for factorising quadratics with a worked example. (The videos explain a process, do you have a different method?)
Factorising quadratics
Factorising harder quadratics
1. Simple Squares: Look at the quadratic equation = 0. It seems to be a perfect square! How can you identify perfect squares? What does the graph of a perfect square parabola look like?
2. Significance of Signs: How does the sign of the solutions relate to the original equation?
3. Reverse Engineering: Imagine you're a mathematician who loves the number 3. Create a quadratic equation that has 3 and -3 as its solutions. What does your equation look like?
4. Creative Coefficients: Design your own factorable quadratic equation. Challenge a friend to factor it. Can they do it without using the quadratic formula?
5. Quadratic Challenge: Find a quadratic equation that is impossible to factor with whole numbers. What does the graph of such an equation look like?
Factorise the quadratic equation .
Factorise the quadratic equation .
Factorise the quadratic equation .
Factorise the quadratic equation .
Factorise the quadratic equation .

