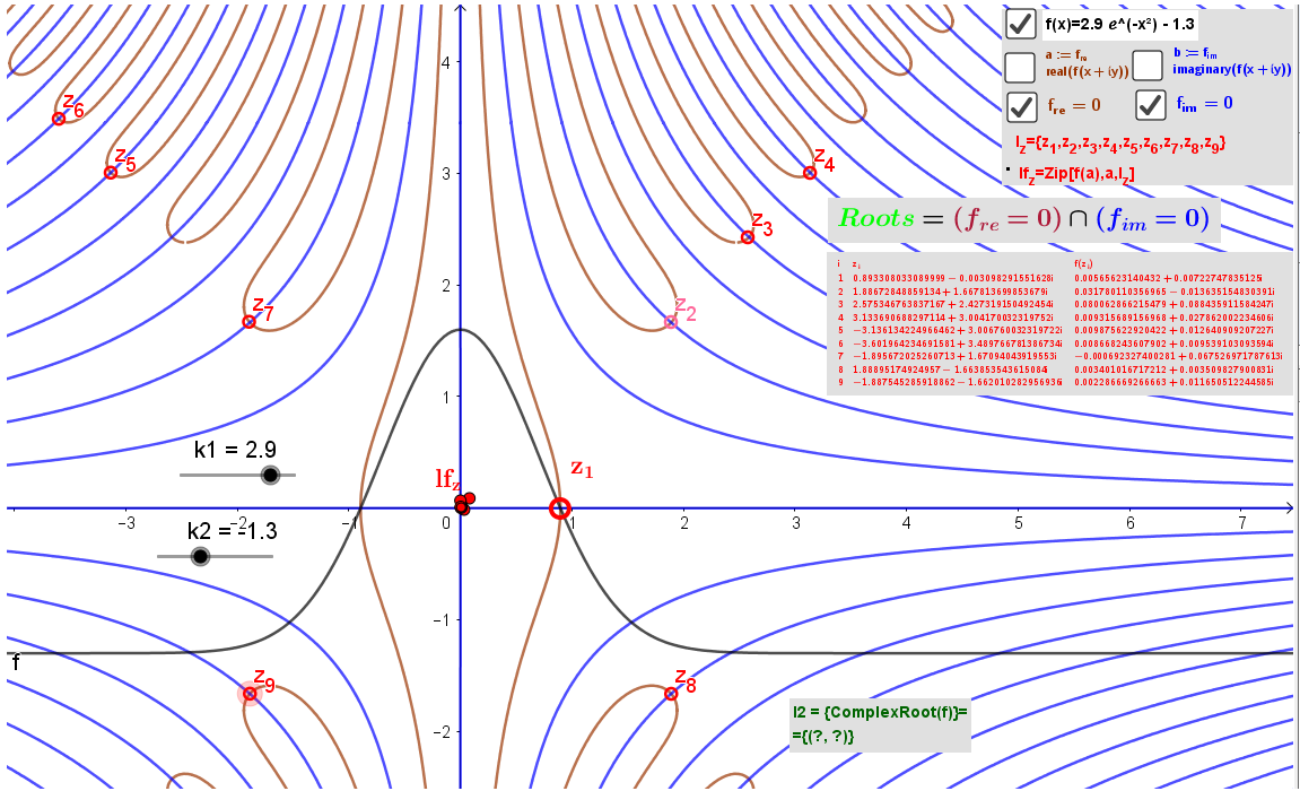
Graphical interpretation and visualizing the Complex Roots of Transcendental functions with Real Coefficients.
Enter the values of the coefficients a and b of the Transcendental function and find its Roots.
Graphical interpretation the Roots: the intersection of implicit functions, which are the zeroed real and imaginary parts of the complex function f(z), respectively: real(f(z))=0 and imaginary(f(z))=0.
In the general case, these roots can be found numerically. Here, one can explore them by moving the test point z to the intersection points of the considered implicit functions and make sure that in these cases, fz=f(z) is at the origin i.e. z ist the root of the original equation.
Another example can be found in the applet https://www.geogebra.org/m/nff3yaah
*New version available.