M9: Einstieg quadratische Funktionen
Quadratische Funktionen im Alltag: Wie schnell fällt ein Stein vom Eiffelturm?
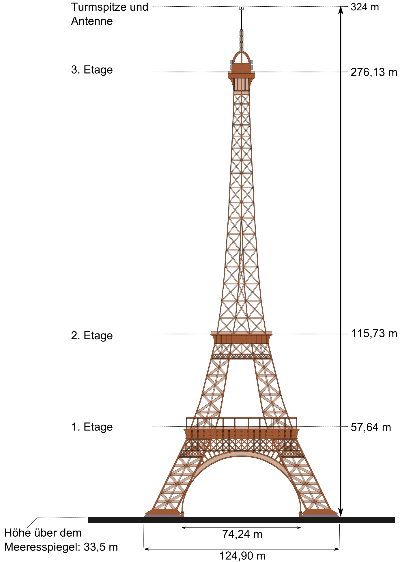
Ein Stein wird vom Eiffelturm fallen gelassen. Um seinen Flugverlauf festzuhalten, wurde der Stein mit einer Uhr und einem Höhenmesser ausgestattet. Der Höhenmesser zeigt an, wie viele Höhenmeter der Stein pro Sekunde zurücklegt. Den Flugverlauf kannst du dir in dem GeoGebra-Applet anzeigen lassen.
(Zur Vereinfachung der Aufgabe wurde der Zusammenhang stark vereinfacht.)
Abnehmende Höhenmeter pro Sekunde
1. Die abnehmenden Höhenmeter pro Sekunde wurden durch das Gerät aufgezeichnet.
Bewege den Schieberegler zu Punkt A und lasse dir die abnehmenden Höhenmeter pro Sekunde in der dazugehörigen Wertetabelle anzeigen (Klicke dazu erst auf den Schieberegler und bewege ihn dann entweder über die Pfeiltaste auf der Tastatur oder mit der Maus).
Fülle hierzu die Tabelle aus:
2. Wie hängen Zeit und abnehmende Höhenmeter zusammen? Stelle einen Funktionsterm auf.
3. Die Aussichtsplattform des Eiffelturms liegt bei 276 m. Nach wie vielen Sekunden kommt der Stein am Boden an, wenn er von dieser Höhe fallen gelassen wird?
Zeit in sek.
0 1 2 3 4 5 6
abnehmende Höhenmeter
Infotext: Einführung quadratischer Funktionen
Eine Funktion f ordnet jedem x-Wert genau einen y-Wert zu. Quadratische Funktionen werden mit dem Funktionsterm f(x) = beschrieben. Gibt man in die quadratische Funktion einen x-Wert ein, erhält man in der Wertetabelle den dazugehörigen y-Wert der quadratischen Funktion f(x). Das dazugehörige Schaubild nennt man Parabel.
Beim Schaubild der Funktion spricht man von der Normalparabel. Bei der Normalparabel liegt der Scheitel im Koordinatenursprung.