L'andamento della funzione e ricerca degli estremi

Grazie ai teoremi di Rolle, Cauchy e di Lagrange, ed alle conseguenze di quest'ultimo, siamo giunti alla seguente importante conclusione: SE

in un certo intervallo la derivata di una funzione ha segno sempre positivo
In quell'intervallo la funzione è continua e derivabile

ALLORA la funzione è crescente. (se il segno della derivata è sempre negativo, la funzione sarà decrescente) Possiamo allora definire una procedura per studiare l'andamento di una funzione per tutti i valori in cui è definita, cioè scoprire per quali di essi è crescente e per quali è decrescente. Procediamo così: calcolata la derivata della funzione, ne studiamo il segno, ovvero calcoliamo per quali intervalli dell'input

è positiva e per quali è negativa. Nei primi avremo che la funzione è crescente, mentre negli altri sarà decrescente. Il teorema di Lagrange ci ricorda che dobbiamo fare attenzione ai punti di discontinuità e di non derivabilitá, perché essi rendono non valido il teorema e quindi ci impediscono di trarre conclusioni dell'andamento della funzione. Di fatto però il problema è facilmente risolvibile: se in un intervallo, in cui ad esempio la derivata è positiva, dovesse esserci un punto di discontinuità, otterremo semplicemente l'effetto di spezzare questo intervallo in due intervalli separati, in ognuno dei quali la funzione è continua e derivabile. Lo chiariamo nel prossimo esempio. ESEMPIO Consideriamo a titolo di esempio la funzione

. La funzione può essere espressa come

, e quindi la sua derivata è

, cioè

. Questa funzione è un quadrato preceduto da un segno meno, e quindi è negativa per qualsiasi valore di

, da cui si potrebbe dedurre che la funzione è sempre decrescente per qualsiasi

Di fatto in tutte le funzioni più semplici i punti che violano il teorema di Lagrange corrispondono a "buchi" nel dominio, e quindi vengono esaminati ben prima di arrivare al calcolo ed allo studio del segno della derivata: vengono rimossi dal piano cartesiano e se ne studiano i limiti corrispondenti. Inoltre spesso in questi punti non esiste neppure la derivata, il che rende piuttosto automatico escluderli dallo studio della stessa, costruendo così il grafico dell'andamento della funzione nel modo corretto. Detto ciò, è comunque importante tenere presente questo aspetto per impostare correttamente lo studio del segno della derivata e dei tratti di monotonia crescente e decrescente della funzione. Nella seguente animazione, infine, vediamo come nel caso in cui il dominio abbia dei confini sia importante cercare gli eventuali punti di estremo anche ai confini del dominio.

Un altro esempio in questo senso è la funzione

Considerando il solo segno della derivata, che in questo caso risulta essere sempre negativo, si sarebbe indotti a credere che la funzione sia sempre decrescente.

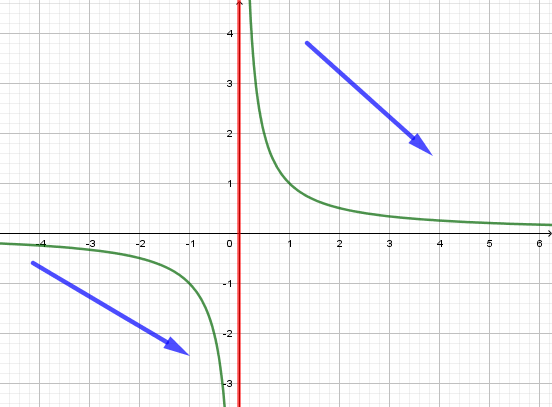
È però importante notare che la funzione ha un punto di discontinuità in

, in questo caso dato dalle C.E. che richiedono che

e del quale quindi ci dovremmo essere accorti ben prima dello studio della derivata nel corso dello studio di funzione. Inoltre la derivata stessa non esiste in , quindi un corretto studio del segno prevede che l'unico intervallo visto precedentemente venga spezzato in due intervalli, separati dal punto

in cui la derivata non è nè positiva nè negativa in quanto non esiste. In entrambi questi intervalli la derivata risulta negativa e quindi si ha l'andamento mostrato qui sotto.

Tenendo conto del punto di discontinuità non abbiamo più un unico intervallo in cui la funzione è decrescente ma due. La derivata NON permette di capire come si comporti la funzione tra un intervallo e l'altro, che dovrà essere dedotto da altri calcoli - in questo caso i limiti al confine del dominio [math]\lim_{x \to 0^-} f(x)[/math] e [math]\lim_{x \to 0^+} f(x)[/math] — Tenendo conto del punto di discontinuità non abbiamo più un unico intervallo in cui la funzione è decrescente ma due. La derivata NON permette di capire come si comporti la funzione tra un intervallo e l'altro, che dovrà essere dedotto da altri calcoli - in questo caso i limiti al confine del dominio e

Il nuovo andamento individuato corrisponde effettivamente con quello della funzione, che è l'ìperbole riferita agli asintoti ed ha il grafico mostrato sotto, in cui è sottolineato l'andamento della derivata.

L'andamento della funzione e ricerca degli estremi

Nuove risorse

Scopri le risorse

Scopri gli argomenti