REİNMANN TEOREMİ
GİRİŞ
19. yüzyılda Mısırda padişahın isteği üzerine ülkenin ileri gelen Matematikçileri ve Mimarları bir araya gelerek Nil nehri üzerine bir köprü kurmaya karar verirler.
Ancak Nil nehrinde belli dönemlerde yaşanan su taşkınları yapılacak köprünün su altında kalma riskini de beraberinde getirir. Bu sorun üzerine düşünen Matematikçiler ve Mimarlar köprü ve nehir arasında kalacak alanın hesaplanmasını ve olası su taşkınlarında köprünün her zaman su üstünde kalmasını sağlamak isterler.
Fakat Nil nehrinin uygun olmayan coğrafi şartları nedeniyle köprü ve nehir arasında kalan alanın her zaman yapıldığı gibi üçgen ve yamuk çogensel alanların yardımıyla hesaplanamaz hale getirmiştir. Bunu üzerine bu alanın tam olarak hesaplanamayacağına karar veren heyet yeni bir yöntem arayışına girer.

Siz olsaydınız doğrusal olmayan köprü ile nehir arasındaki mesafeyi hangi yöntem ile yaklaşık olarak hesaplardınız?
KEŞFET
Aşağıda verilen materyalleri inceleyiniz ve kutucukları sırası ile tıklayınız.
Aşağıda verilen düzgün olmayan şeklin alanını yaklaşık olarak en az kaç birim kareden oluştuğunu bulmaya çalışınız.
Aşağıda verilen düzgün olmayan şeklin alanını yaklaşık olarak en fazla kaç birim kareden oluştuğunu bulmaya çalışınız.
Bu iki şeklin alanı yaklaşık olarak kaç birim kare olabilir ?
Bu şekillerde neden geometrik şekil ile yaklaşık alan bulma yöntemi kullanıldı ?
Şekilde verilen f(x) ile x ekseni arasında kalan alanı bulunuz.
Aşağıda verilen doğrusal olmayan eğrinin x ekseni arasında kalan alanı yaklaşık olarak bulunmasını inceleyiniz..
Yukardaki şekillerin alanları bulunurken hangi yöntemler kullanılmıştır?
Son verilen şeklin alanının çokgensel alanların yardımıyla tam olarak bulunamama nedeni sizce nedir ?
AÇIKLAMA
Buraya kadar size öğretmeye çalıştığım bir eğrinin altında kalan alanı buldurmaya çalışmaktı.
y=f(x) sürekli bir fonksiyon olmak üzere , y=f(x) fonksiyonunun grafiği ile x ekseni arasında kalan ve x=a ile x=b doğrularının sınırlandırdığı bölgenin alanı :
1.) y=f(x) grafiği doğrusal bir grafik olduğu zaman üçgen , yamuk gibi çokgensel alanlarlar yardımıyla bulunabilinir.
2.) y=f(x) grafiği doğrusal bir grafik olmadığı zaman alanı nasıl bulabiriz?
yukarıdaki verdiğim örneklere baktığımızda eğrisel bir şeklin alanını geometrik şekiller yardımıyla parçalayıp yaklaşık değerini bulabiliriz. Burada devreye giren REİMANN toplamı alanı bulmak için genel bir yöntem olup her türlü grafiğe sahip fonksiyonlarda kullanılabilinir.
Reimann Toplamı
Riemann toplamı, bir eğrinin altındaki alanı çok sayıda dikdörtgene bölerek belirlenmiş olan, bu alanın yaklaşık değeridir.
![[size=150]Riemann eğrinin altındaki alanı dikdörtgenlere ayırmış ve bu seferde gerçek alandan az olduğunu anlamış.[/size]](https://www.geogebra.org/resource/nhkksygr/FoXYg7TKaZYvvMki/material-nhkksygr.png)
![[size=150]Riemann eğrinin üstündeki alanı dikdörtgenlere ayırmış ve bu seferde gerçek alandan fazla olduğunu anlamış.[/size]](https://www.geogebra.org/resource/xmtz8kwh/8kLRhg10blJslptT/material-xmtz8kwh.png)
Riemann bu girişimleri ışığında gerçek alanın alt toplam ile üst toplam değeri arasında olacağına kanaat getirmiş.
Aşağıdaki kutucuklara tıklayarak reimann toplamının gerçek alan değerine ne kadar yakın olduğunu inceleyiniz.
DERİNLEŞTİRME
Aşağıda verilen şekilde sürgüyü hareket ettirerek sayısal verilerdeki değişimi inceleyiniz.
yukarıdaki şekli incelediğimizde bölme sayısı olan "n" nin değeri arttırıldığında alt toplam ve üst toplam değerlerinin gerçek alan değerine dahada yaklaştıklarını fark ettiniz mi ?
DEĞERLENDİRME
Aşağıdaki soruları cevaplamaya çalışınız.bulduğunuz sonucu kutucuğa tıklayarak kontrol ediniz.
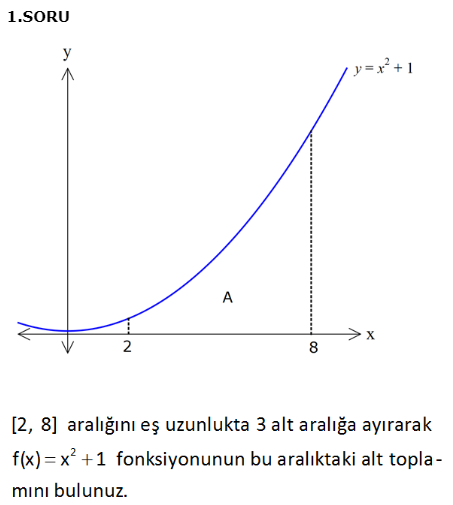
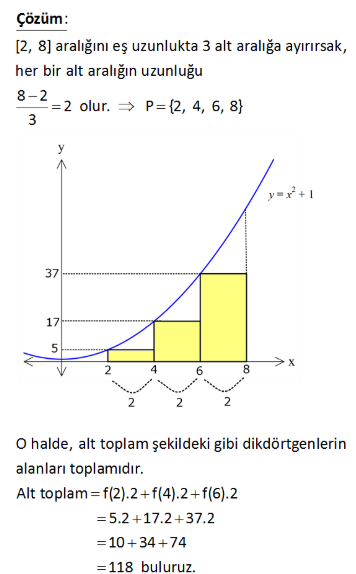
1.SORU
1.ÇÖZÜM
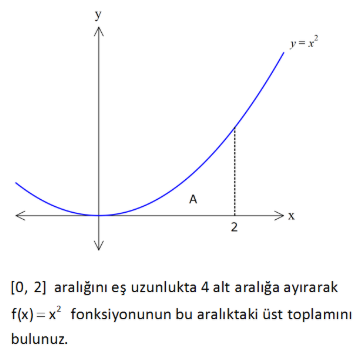
2.SORU
