Demonstration of Pythagorean Theorem
Introduction
The Pythagorean theorem states that , where and represent the lengths of the two shorter legs of a right triangle and represents the length of the hypotenuse.
Visualization
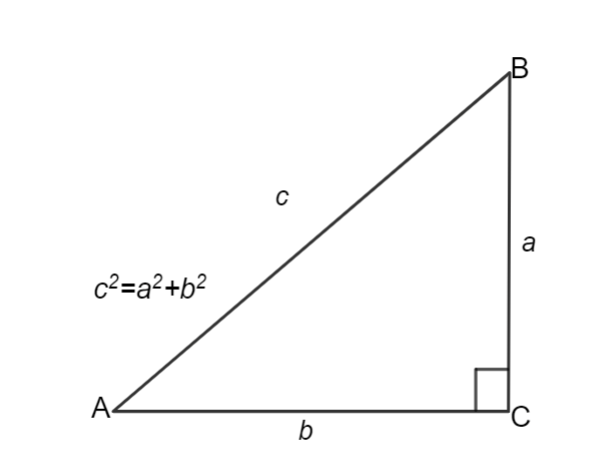
Warm Up:
Play around with the length of the legs to see how the other sides change. Then, answer the 2 multiple choice questions below.
If and , then
If and , then
Making Sense of the Pythagorean Theorem
Relate the Pythagorean Theorem to area by rearranging partitions of a square.
Putting It All Together
Answer these open ended questions with your partner to form deeper math connections.
Move the pink point at the top of the figure. When you change the lengths of sides and , what effect does that have on the length of side ?
How is the size of the square with area affected?
Now, move the second point as far over as you can. How are the sizes of the squares with area and affected?
If you were able to make a right triangle with legs that had lengths of , and , what can you say about the area of a square with side lengths equal to ?
Generalize the relationship between the areas of the squares with side lengths , , and .