Messdatenerfassung mit Geogebra (individuell bearbeitbar)
Diese Aktivität ist an Lehrkräfte gerichtet.
TL;DR
Dieses Applet ist zur Messdatenauswertung im (Physik-)Unterricht. Für die Verwendung ist ein Geogebra-Account der Lehrkraft notwendig.
Das Applet kann entweder so verwendet werden, wie es ist (drei Punkte oben rechts -> Aktivität kopieren, eine Kopie der Aktivität ist nun im Profil gespeichert) oder angepasst werden wenn die Spalten eine andere Reihenfolge haben sollen/ mehrere Messreihen aufgenommen werden sollen/ ... (siehe unten).
Ziel und Motivation
Ziel ist es, digitale Messdatenerfassung und -auswertung in Geogebra durchzuführen. Einerseits können Lehrkräfte das Projekt nutzen (Beamer im Klassengespräch), andererseits können SuS mit Tablets oder Laptops Messdaten erfassen und auswerten.
Aufbau
Das Applet ist folgendermaßen aufgebaut:
- Tabelle: Hier werden die Messdaten und Fehler eingetragen
- Grafik: Hier werden die Messdaten, Fehler und ggf. der Fit geplottet
- Algebra-Fenster: Hier liegt der Code. Dieser wird unten ausführlich erklärt
Bearbeiten des Applets
Um das Applet anzupassen, benutze entweder das Programm (Geogebra Classic 6). Dafür klicke auf die drei Punkte oben rechts in dieser Aktivität und wähle "Aktivität kopieren". Jetzt ist die Aktivität in Deinem Profil gespeichert. Bist Du im Programm mit Deinem Account angemeldet, erscheint die Aktivität jetzt in deinem Profil (Hamburgermenu -> Öffnen). Oder benutze die Website: Dafür einfach auf die drei Punkte oben rechts in dieser Aktivität klicken und "Mit App öffnen".
Nach Bearbeitung gehe auf Speichern (Hamburgermenu -> Speichern). Die Aktivität wird in deinem Profil gespeichert. Für eine lokale Speicherung auf dem Gerät gehe auf Herunterladen als Geogebra Datei (Hamburgermenu -> Herunterladen als Geogebra Datei).
Algebra Fenster öffnen
Um das Applet anzupassen, muss das Algebra Fenster geöffnet werden (hier steht der Code). Dafür klicke auf das Hamburgermenu oben rechts, dann auf "Ansicht". Nun setze einen Haken bei "Algebra". Ist das Fenster zu klein, so kannst Du den Trennbalken zwischen den Fenstern verschieben.
Individuelle Anpassung
Angepasst werden kann, in welcher Spalte die Daten stehen, also welche Spalte die x-Daten, y-Daten und jeweiligen Fehler beinhaltet. Bitte ändere den Code nicht (außer du weißt, was du tust), sondern nur die folgende Objekte:
x_{Spalte}={<x-Daten der ersten Messreihe>,<x-Daten der zweiten Messreihe>,...}gibt an, in welcher Spalte die x-Werte stehen. Sind mehrere Werte in der Mengenklammer, so werden die Werte als verschiedene Messreihen interpretiert (Reihenfolge ist wichtig)y_{Spalte}={<y-Daten der ersten Messreihe>,<y-Daten der zweiten Messreihe>,...}gibt an, in welcher Spalte die y-Werte stehen. Sind mehrere Werte in der Mengenklammer, so werden die Werte als verschiedene Messreihen interpretiert (Reihenfolge ist wichtig)
x_{Spalte}={1,3} und y_{Spalte}={2,4} bedeutet, dass es zwei Messreihen gibt, wobei die erste Messreihe in Spalten 1, 2 ist und die zweite Messreihe in Spalten 3,4 ist (x links, y rechts)
err_x={<x-Fehler der ersten Messreihe>,<x-Fehler der zweiten Messreihe>,...\}gibt an, in welcher Spalte die x-Fehler stehen. Sind mehrere Werte in der Mengenklammer, so werden die Werte als verschiedene Messreihen interpretiert (Reihenfolge ist wichtig). Soll eine Messreihe keinen Fehler haben, so kann eine Null an dieser Stelle eingesetzt werdenerr_y=err_x={<y-Fehler der ersten Messreihe>,<y-Fehler der zweiten Messreihe>,...\}gibt an, in welcher Spalte die y-Fehler stehen. Sind mehrere Werte in der Mengenklammer, so werden die Werte als verschiedene Messreihen interpretiert (Reihenfolge ist wichtig). Soll eine Messreihe keinen Fehler haben, so kann eine Null an dieser Stelle eingesetzt werden
x_{Spalte}={1,1,1} , y_{Spalte}={2,3,4} , err_x={}, err_y={5,5,6} bedeutet, dass es drei Messreihen gibt. Alle Messreihen haben die x-Daten in Spalte 1, die y-Daten stehen in Spalte 2, 3 und 4. Es gibt keine x-Fehler. Die y-Fehler auf Messreihe 1 und 2 (die in Spalte 2 und 3 sind) sind in Spalte 5, die x-Fehler auf Messreihe 3 (in Spalte 4) sind in Spalte 6.
Abschluss
Sind alle gewünschten Änderungen vorgenommen, so
- schließe das Algebrafenster (Hamburgermenu -> Ansicht).
- Benenne gegebenenfalls die Spalten der Tabelle neu (aber achte darauf, dass der Tabellenkopf drei Zeilen umfasst, also die Daten erst ab Zeile 4 beginnen).
- Verschiebe die Skala des Koordinatensystems so, dass sie für das Experiment geeignet ist (können die SuS aber auch selbst tun), indem du mit gedrückter Shift Taste die Achse skalierst.
- Die Achsenbeschriftung, falls gewollt, findet sich in den Einstellungen der Grafik.
- Verschiebe die Trennwand zwischen Tabelle und Grafik so, dass die Breite der Tabelle genau passt.
Speichern
Für eine ausführliche Erklärung, siehe Geogebra Einführung (Tutorials -> Erstellung einer Unterrichtseinheit).
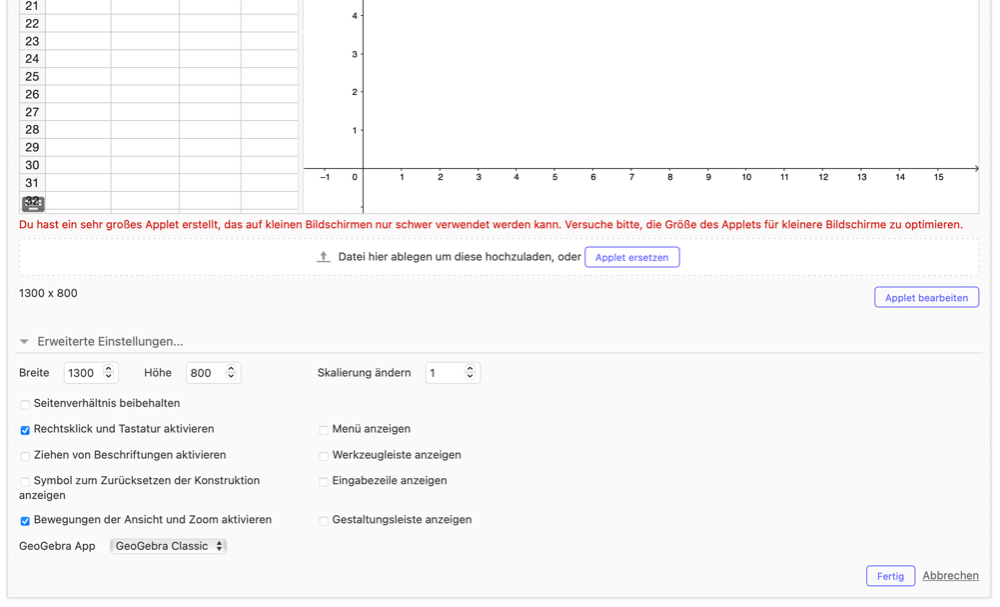
Zusammengefasst: Das Applet kann gesichert werden, indem im Hamburgermenu "Datei" und dann "Speichern" ("Geteilt" auswählen) ausgewählt wird. Dem Applet kann nun ein Name vergeben werden und es wird im Profil gespeichert. Jetzt muss nochmal die Aktivität im Profil geöffnet werden. Wähle dafür bei den drei Punkten "Aktivität bearbeiten" und fahre mit der Maus über das Applet. Klicke auf den Stift über dem Applet, das erschienen ist. Unter "Erweiterte Einstellungen" müssen nun ein paar Dinge eingestellt werden (siehe Bild unten):
- Größe des Applets: Die Größe des Applets sollte nicht breiter als 1400 sein, man sollte jedoch alles gut sehen (sowohl Tabelle, als auch genug von der Grafik). Das Applets sollte auch nicht zu quadratisch sein; im Vollbildmodus sollte es circa passen. Das Applet unten hat die Maße 1300x800
- Rechtsklick und Tastatur aktivieren: Nur so kann die Tabelle bearbeitet werden, also Daten eingefügt werden (Rechtsklick ist für Copy Paste notwendig)
- Bewegung der Ansicht und Zoom: Damit kann die Grafik verschoben und gezoomt werden
- Rest: Sollte ausgestellt werden. Die Funktionen des Applets sind auf das beschränkt, das verändert werden soll. Bspw. eine Werkzeugliste würde eher verwirren und ist einfach unnötig
-----------------------------------------------------------------------------------------------
In Depth: Befehle
In Geogebra können Zellen der Tabelle mit dem Befehl Zelle(i,j) (Spalte i, Zeile j) referenziert werden. Somit kann eine Liste mit Datenpunkten (wobei Spalte 1 die x-Daten und Spalte 2 die y-Daten enthält) mit dem Befehl
Data1=Folge((Zelle(1,j),Zelle(2,j)),j,1,n})
erstellt werden. n kann als Variable im Algebrafenster oder als Schieberegler im Grafikfenster definiert werden (Wird n als Schieberegler im Grafikfenster definiert, so ist es sinnvoll, diesen entsprechend zu benennen (z.B. "Anzahl der Datenpunkte"). Der Schieberegler ist dann zum Verschieben durch die SuS gedacht. Wird er nur im Algebrafenster definiert, so empfiehlt es sich, n auf einen großen Wert zu setzen, z.B. n=50 oder n=100, da sonst eine lange Datenreihe einfach abgeschnitten wird). Analog kann für die restlichen Datenreihen Data2 usw. erstellt werden.
Um (bei einem anderen Experiment) die Spaltenreihenfolge zu ändern, muss die erste Zahl im Zelle Befehl verändert werden. Da es sehr umständlich wäre, immer im Befehl selbst die Nummer der Spalte zu ändern, wird dies mit Variablen geregelt: Es werden die Mengen
x_{Spalte}={...}
y_{Spalte}={...}
in Geogebra definiert (Mengen mit beliebig vielen Elementen). Die k-te Zahl der Menge x_{Spalte} korrespondiert dann zu den x-Daten der k-ten Messreihe. Dies entspricht dem Befehl x_{Spalte}(k) in Geogebra. Außerdem sollen die ersten drei Spalten der Tabelle frei bleiben für Notizen, die zu messende Größe und Einheit. Die neuen Befehle lauten nun
Data1=Folge((Zelle(x_{Spalte}(1),3+j),Zelle(y_{Spalte}(1),3+j)),j,1,n)
Data2=Folge((Zelle(x_{Spalte}(2),3+j),Zelle(y_{Spalte}(2),3+j)),j,1,n)
...
Es können beispielsweise fünf Datenreihen über diese Befehle definiert werden. Enthält die Menge x_{Spalte} oder y_{Spalte} weniger Elemente, so ist Data5 nicht definiert und wird nicht angezeigt. Somit kann einfach mehr programmiert werden, als benötigt wird und es müssen nicht im Anschluss neue Befehle ausgedacht werden.
Die Fehlerbalken bestehen aus Strecken, die von dem jeweiligen Datenpunkt ausgehen. Mit x- und y-Fehlern entsteht so ein Kreuz. Der waagerechte Teil des Kreuzes lässt sich mit
Folge(Strecke(
Data1(j)-(Zelle(err_{x}(1),3+j),0),
Data1(j)+(Zelle(err_{x}(1),3+j),0)
),j,1,n)
erzeugen. Analog lässt sich der senkrechte Teil mit Folge(Strecke(
Data1(j)-(Zelle(err_{y}(1),3+j),0),
Data1(j)+(Zelle(err_{y}(1),3+j),0)
),j,1,n)
erzeugen. Um zu viele verschiedene Objekte in der Algebraansicht zu vermeiden, werden diese beiden Befehle in einem Objekt definiert (Beide Objekte mit einer Mengenklammer verbinden). Der neue Befehl lautet schließlich
Err1={Folge(Strecke(
Data1(j)-(Zelle(err_{x}(1),3+j),0),
Data1(j)+(Zelle(err_{x}(1),3+j),0)
),j,1,n),
Folge(Strecke(
Data1(j)-(0,Zelle(err_{y}(1),3+j)),
Data1(j)+(0,Zelle(err_{y}(1),3+j)
),j,1,n)}
Für die restlichen Datenreihen kann Err2 usw. analog definiert werden
Die verschiedenen Daten können im Algebrafenster verschieden eingefärbt werden (hier: Regenbogen)
Weiterführende Ideen
Eine einfache Implementierung der Funktionenanpassung wäre, eine Funktion zu definieren, die von einem oder mehreren Schiebereglern abhängig ist. Die Schieberegler sind in der Grafikansicht zu sehen und können durch die SuS verschoben werden. So kann (ohne großes programmieren) spielerisch gezeigt werden, wie Funktionenanpassung (ungefähr) funktioniert. Dabei können außerdem die Fehler thematisiert werden.
Eine andere Möglichkeit der Funktionenanpassung wäre, eine Funktion in Abhängigkeit von mehreren Variablen zu definieren, bspw
f(x,a,b,c)=ax+b/y+c . Mithilfe einer Schaltfläche und JavaScript kann nun eine "echte" Funktionenanpassung (mit Berücksichtigung der Fehler) mit Abstandsmaß programmiert werden und die Parameter der Funktion a, b, c mit Fehlern auszugeben