Conceitos
Ao falarmos sobre triângulos retângulos, a primeira propriedade que vem à cabeça de muitos de vocês, certamente, é o Teorema de Pitágoras. Mas, apesar de sua beleza e aplicabilidade, o Teorema de Pitágoras não é a única propriedade importante dos triângulos retângulos.
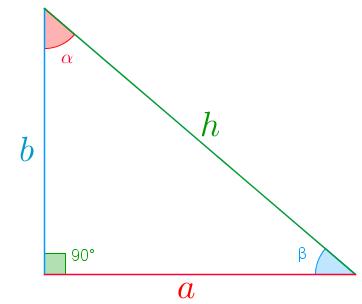
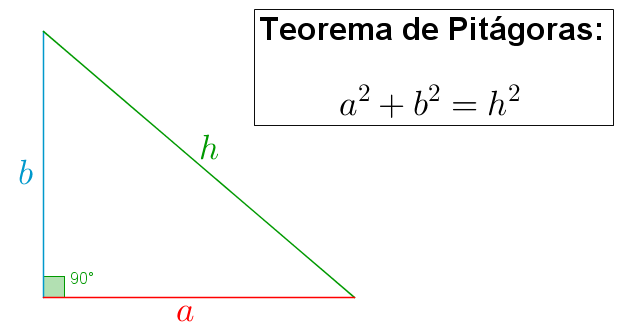Nesta Sala de Estudos, vamos explorar os triângulos retângulos utilizando ferramentas da Geometria como, por exemplo, semelhança, para obtermos várias propriedades interessantes e largamente utilizadas em medições indiretas. E, diferentemente do Teorema de Pitágoras, que utiliza apenas as medidas dos lados dos triângulos retângulos, aqui utilizaremos também as medidas dos dois ângulos agudos desses triângulos, já que o início das nossas discussões será estabelecer, de alguma forma, relações entre as medidas dos lados e dos ângulos internos de um triângulo retângulo.
O ramo da matemática que estuda relações entre ângulos e lados de um triângulo é a Trigonometria.
A palavra trigonometria vem do grego – τριγωνομετρία – que é a composição das palavras gregas τρίγωνον(trigonon: triângulo) e μέτρον (metron: medida). A primeira dessas, por sua vez, é composta das palavras τρεῖς, τρία(tris, tría: três) e γωνία (gonia: ângulo).
Assim, utilizaremos os significados dos três radicais gregos que formam a palavra Trigonometria
tri (três) + gonos (ângulos) + metron (medidas)
para apresentar o objetivo central desta Sala de Estudos:
estudar medições em triângulos.
A Trigonometria atua direta ou indiretamente em vários ramos da Matemática que requerem medidas de precisão e tem numerosas aplicações na Astronomia, na Topografia, no estudo de imagens digitais, em sistemas de navegação por satélites, e, de maneira geral, na determinação de ângulos e de distâncias inacessíveis. Nesta sala, apresentaremos algumas das aplicações geométricas da Trigonometria.
E se vocês estão habituados a ver a palavra trigonometria em tópicos do ensino médio, não se preocupem: para entender o que vai ser tratado aqui, vocês só precisam saber um pouco sobre triângulos!
Nesta Sala de Estudos, vamos explorar os triângulos retângulos utilizando ferramentas da Geometria como, por exemplo, semelhança, para obtermos várias propriedades interessantes e largamente utilizadas em medições indiretas. E, diferentemente do Teorema de Pitágoras, que utiliza apenas as medidas dos lados dos triângulos retângulos, aqui utilizaremos também as medidas dos dois ângulos agudos desses triângulos, já que o início das nossas discussões será estabelecer, de alguma forma, relações entre as medidas dos lados e dos ângulos internos de um triângulo retângulo.
O ramo da matemática que estuda relações entre ângulos e lados de um triângulo é a Trigonometria.
A palavra trigonometria vem do grego – τριγωνομετρία – que é a composição das palavras gregas τρίγωνον(trigonon: triângulo) e μέτρον (metron: medida). A primeira dessas, por sua vez, é composta das palavras τρεῖς, τρία(tris, tría: três) e γωνία (gonia: ângulo).
Assim, utilizaremos os significados dos três radicais gregos que formam a palavra Trigonometria
tri (três) + gonos (ângulos) + metron (medidas)
para apresentar o objetivo central desta Sala de Estudos:
estudar medições em triângulos.
A Trigonometria atua direta ou indiretamente em vários ramos da Matemática que requerem medidas de precisão e tem numerosas aplicações na Astronomia, na Topografia, no estudo de imagens digitais, em sistemas de navegação por satélites, e, de maneira geral, na determinação de ângulos e de distâncias inacessíveis. Nesta sala, apresentaremos algumas das aplicações geométricas da Trigonometria.
E se vocês estão habituados a ver a palavra trigonometria em tópicos do ensino médio, não se preocupem: para entender o que vai ser tratado aqui, vocês só precisam saber um pouco sobre triângulos!