Derivative of circle area (a Calculus-Geometry connection)
Consider a circle with radius r. The area of the circle is given by the formula A = _____. The circumference of the circle is given by the formula C = _____.
Let dA be the infinitesimal change in area A that results from dr, an infinitesimal change in radius r. How does the animation below informally illustrate why the derivative of circle area A is what it is?
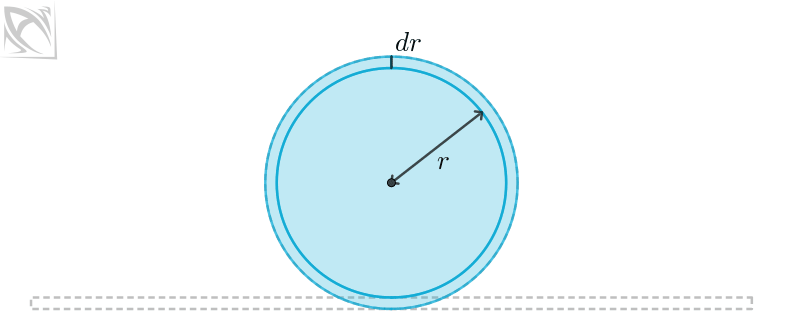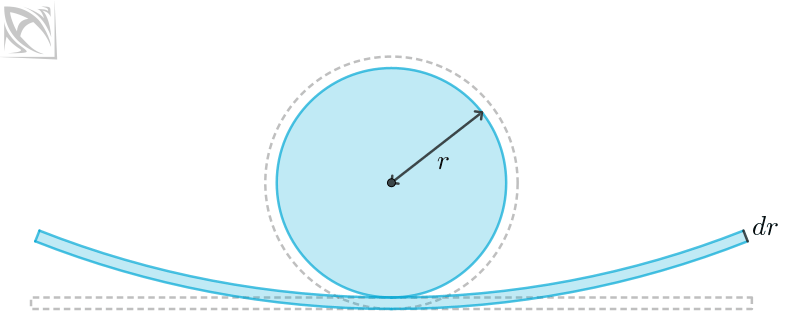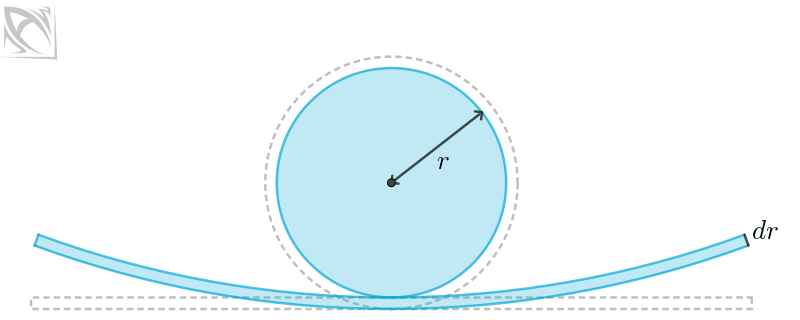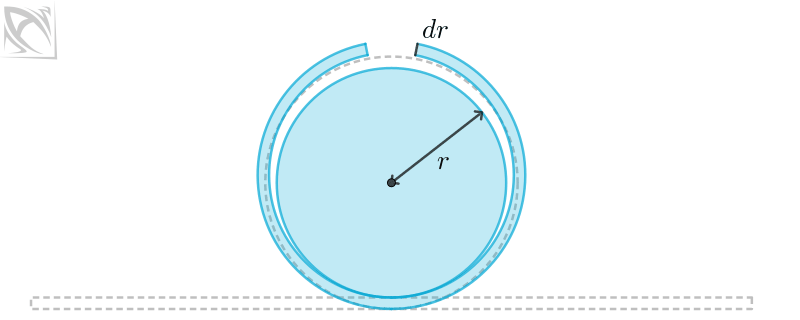
Use the slider in the construction below if you prefer to animate this yourself (You control freak).
This demonstration seems to primarily make a connection in the realm of derivative calculus, but it also serves as a good precursor to later studies in integral calculus. If a student has only studied derivatives as a ratio dy/dx, this illustrates that a single differential such as dr may be interpreted on its own without being part of a "slope."
The discussion could easily extend to conceptualizing the entire circle as n→∞ layers of such strips, previewing a conceptual groundwork for later use of ∫ to sum up all the n pieces.
Also see Circle Area #1 ("unrolling") construction.
Also, on a related note, this other GeoGebra construction demonstrates a calculus connection between the volume and surface area of a 3D sphere.