Volume of a Solid of Revolution
Disk Method
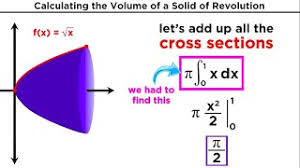
Volumes of Solids of RevolutionYou can also use the definite integral to find the volume of a solid that is obtained by revolving a plane region about a horizontal or vertical line that does not pass through the plane. This type of solid will be made up of one of three types of elements—disks, washers, or cylindrical shells—each of which requires a different approach in setting up the definite integral to determine its volume. Disk method the axis of revolution is the boundary of the plane region and the cross-sections are taken perpendicular to the axis of revolution, then you use the disk method to find the volume of the solid.
Because the cross-section of a disk is a circle with an area π r 2, the volume of each disk is its area times its thickness. If a disk is perpendicular to the x‐axis, then its radius should be expressed as a function of x. If a disk is perpendicular to the y‐axis, then its radius should be expressed as a function of y. The volume ( V) of a solid generated by revolving the region bounded by y = f(x) and the x‐axis on the interval [ a, b] about the x‐axis is
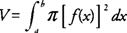If the region bounded by x = f(y) and the y‐axis on [ a, b] is revolved about the y‐axis, then its volume ( V) is
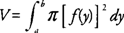Note that f(x) and f(y) represent the radii of the disks or the distance between a point on the curve to the axis of revolution.
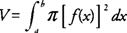If the region bounded by x = f(y) and the y‐axis on [ a, b] is revolved about the y‐axis, then its volume ( V) is
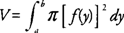Note that f(x) and f(y) represent the radii of the disks or the distance between a point on the curve to the axis of revolution.Washer Method
Washer method the axis of revolution is not a boundary of the plane region and the cross-sections are taken perpendicular to the axis of revolution, you use the washer method to find the volume of the solid. Think of the washer as a “disk with a hole in it” or as a “disk with a disk removed from its center.” If R is the radius of the outer disk and r is the radius of the inner disk, then the area of the washer is π R 2 – π r 2, and its volume would be its area times its thickness. As noted in the discussion of the disk method, if a washer is perpendicular to the x‐axis, then the inner and outer radii should be expressed as functions of x. If a washer is perpendicular to the y‐axis, then the radii should be expressed as functions of y.
The volume ( V) of a solid generated by revolving the region bounded by y = f(x) and y = g(x) on the interval [ a, b] where f(x) ≥ g(x), about the x‐axis is
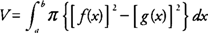If the region bounded by x = f(y) and x = g(y) on [ a, b], where f(y) ≥ g(y) is revolved about the y‐axis, then its volume ( V) is
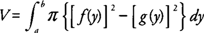Note again that f(x) and g(x) and f(y) and g(y) represent the outer and inner radii of the washers or the distance between a point on each curve to the axis of revolution
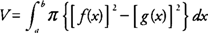If the region bounded by x = f(y) and x = g(y) on [ a, b], where f(y) ≥ g(y) is revolved about the y‐axis, then its volume ( V) is
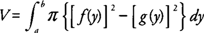Note again that f(x) and g(x) and f(y) and g(y) represent the outer and inner radii of the washers or the distance between a point on each curve to the axis of revolution