Legyen adott...
Mottó
"Van, amit el tudok képzelni, és le tudok rajzolni. Van, amit el tudok képzelni, de nem tudok lerajzolni. De tudnék-e olyat rajzolni, amit nem tudok elképzelni? Ez nagyon érdekel."
Legyen adott egy kocka... és ... egy (szabályos) oktaéder!
Számtalan matematikai és egyéb probléma kezdődhet így. Mit jelent az, hogy adott?
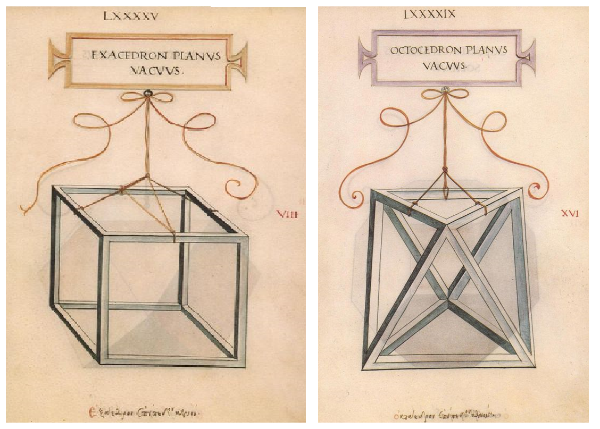
Vegyük a kezünkbe egy modelljét, tegyük az asztalra, rajzoljuk le, esetleg egy-egy zsinórra felfüggesztve, mint azt Leonardo tette? Vagy csak képzeljük el, hogy "ott van" a szemünk előtt?
A "Legyen adott... " kezdetű mondatot értelmezve fel kell tételeznünk, hogy van egy közlő (adó) egy befogadó (vevő) és egy "kommunikációs csatorna" amely arról gondoskodik hogy az adó és a vevő pontosan ugyanazt értse az átküldött "dolog" (fogalom, összefüggés, kapcsolat, stb.) alatt. Maga a "csatorna" lehet egy rajz, leírás, de akár egy egyértelműen megadott számokból álló struktúra (számítógépi program) is, ha a "csatorna" éppen egy számítógép, amely jól -rosszul közvetít az adó és a vevő között.
Ha például a GeoGebra eszköztárát választjuk a címben említett két objektum megjelenítésére (megadására), és befogadására (szemlélésére), és ezt nem szeretnénk elintézni két beépített paranccsal, két egymástól jól elkülöníthető adatszerkezetet kell megadnunk. a program számára. Különösen akkor, ha e két objektum közötti kapcsolatot szeretnénk elemezni.
Először meg kell adnunk a csúcsaik koordinátáit - a GeoGebra koordináta rendszerében-, majd a (kombinatorikus) szerkezetüket, vagyis azt, hogy a megadott pontokat milyen sorrendben megadva kapjuk meg a két objektum lapjait, éleit. Ez történhet fordított sorrendben is - mint jelen esetben, ha a csúcsaik valamilyen módon függenek egymástól. A vevő - jelen esetben e sorok érdeklődő olvasója - megelégedhet a kapott látnivalókkal, amelyeket "interaktívan beavatkozva" módosíthat, alaposan megismerhet. Sőt, ha nagyon elszánt, felfedezhet olyan új összefüggéseket is, amelyekre az "adó" - e sorok írója - talán nem is gondolt.
Minden további fontoskodás helyett nézzük a konkrétumokat. :-)
Bár a geometriában nincs "lent és fent" azért mégis célszerű ezeket az adatokat praktikus módon felvenni, mint azt Leonardo tette. Csak nekünk a GeoGebra 3D-s koordinátarendszeréhez kell igazodnunk. Legyen a két alakzat középpontja az origó, a kocka tengelyei legyenek párhuzamosak a koordinátarendszer tengelyeivel, az oktaéder átlói legyenek a tengelyek.
Az alábbi GeoGebra fájlban máris adunk egy kis feladatot olvasóinknak: alaphelyzetben csak egy pontot látnak. Ezt kicsit megmozgatva az egérrel, találják ki, hogy minek mi a hatása!
Kocka - oktaéder
Vegyük észre, hogy...
... a fenti appleten lévő pontot mozgatva kiderül, hogy a feltáruló négyzeten mozgó ∘ pont a megjelenő kocka és oktaéder, a négyzet oldalán mozgó ▶ pont pedig egy gömb áttetszőségét vezérli.
Közismert, hogy a kocka lapjainak középpontjai egy szabályos oktaédernek, ennek a középpontjai egy kockának a csúcsai. Az appletben megjelent még egy csúszka is, amely mozgatásával a kockának és az oktaédernek egy rögzített, r sugarú gömbhöz - így egymáshoz is - viszonyított mérete változik. Ezt a változást itt az a*b=r2 kapcsolat írja le, ahol (a,a,a) számhármasa kockának, (0,0,b) az oktaédernek egy-egy csúcsát határozza meg.
Ezzel egyértelművé tettük nem csak a magunk, hanem a GeoGebra programunk számára is, hogy miként adott a kocka és vele együtt egy oktaéder.
A csúszkával "kitapogatható" az a speciális eset, amelyben a kocka és az oktaéder egymásnak megfelelő élei nem csak merőlegesek egymásra, hanem metszik is egymást. Ebben az esetben a kocka és az oktaéder test közös része (metszete) az un. kocka-oktaéder.
Ezt a félig szabályos poliédert is ismerte, lerajzolta Leonardo, mi több, Arkhimédész is.
Egy arkhimédészi poliéder: a kocka-oktaéder
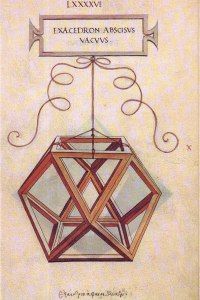
A poliédereknek ezt a szabályos poliédereknél - a platóni testeknél - kissé népesebb (13 tagú) családját, amelyeknek a lapjai szabályosak, de többféle lapjuk is lehet, testszögleteik viszont nem szabályosak, de egybevágók, arkhimédészi testeknek nevezik a matematikusok. Mi most azonban - ezt a szép témát (ideiglenesen) elengedve - más irányba fogunk kalandozni.
A dualitásról
Az első appletben a két szabályos poliédernek egy szorosabb kapcsolatát mutattuk be, ezek egymásnak az r sugarú gömbbel megadott duálisai. A poliéderek közötti duális kapcsolat ennél lényegesen általánosabb összefüggés. Erről itt juthatnak olvasóink kicsit részletesebb ismeretekhez.
Általánosabban egy-egy poliéder duálisának az előállítása két dolgot jelent:
- meg kell keresni egy poliéder hálózatának (kombinatorikus szerkezetének) a duálisát, kihasználva, hogy az eredeti poliéder csúcsainak a keresett poliéder lapjai, lapjainak a csúcsai, éleinek az élei felelnek meg;
- meg kell adni egy olyan- többnyire egy gömbbel meghatározott - térbeli polaritást, amely a tér pontjaihoz síkokat, síkjaihoz pontokat, egyeneseihez egyeneseket rendel illeszkedéstartó módon, majd ezzel meg kell (kellene?) határozni a duális poliéder csúcsait.
Én a klónom vagyok
E sorok írója ezt a bizarr állítást az utcán olvasta egy játékos - talán filozofikus - hajlamú fiú pólóján.
Hmm. Aki ilyet állít magáról, és ezt közhírré is teszi, minden bizonnyal tud valamit a halmazelmélet és a logika antinómiáiról.
Játsszunk mi is egy kicsit! Csak itt és most -házi használatra szánt - fogalomként vezessünk be néhány - a klónozásra hajazó - összefüggést. Itt most a klón szót a másolat, megkettőzés értelemben használjuk, ami olykor tilos, bár a matematikában kevésbé. Még talán örülhetünk is neki.
Nevezzünk egy poliédert klónozásra alkalmasnak, ha p3 háromszög, p4 négyszög,... pn n-szög lapja, és ugyancsak p3 háromélű, p4 négyélű, ... pn n élű csúcsa van. Ilyen például a szabályos tetraéder, általában az n oldalú gúla, vagy az összes olyan tórusz-szerű poliéder, amelynek minden lapja négyszög és minden csúcsába 4 él fut be.
Egy klónozásra alkalmas kombinatorikus szerkezetű, és alkalmasan megadott csúcsokkal egyértelművé tett poliéder klónjának nevezzük azt, amelyhez van olyan gömb, amelyre vonatkozó polaritással előáll az eredetivel egybevágó duális poliéder. Olykor igen nehéz feladat ilyen poliédert találni. Az is előfordulhat, hogy hiába alkalmas egy poliéder klónozásra, még sem tudjuk (esetleg nem is lehet) úgy megadni a csúcsait, hogy a duálisa a klónja legyen.
De van ennél nehezebb kérdés is. Vajon van-e olyan poliéder, amely egybeesik a klónjával, mint ahogy ezt az említett fiatalember állította magáról?
Egy kis (?) segítség...
Először keressünk egy klónozásra alkalmas kombinatorikus szerkezetű poliédert.
Segítségért - tunya, melankolikus módon - mindjárt forduljunk az örök ifjú, Albrect Dürerhez, aki 43 évesen többek között megajándékozott bennünket egy híres poliéderrel, amelyről azóta is jóízűen vitatkoznak a matematikusok, de nem csak ők. Sőt
!
Az mindenki számára nyilvánvaló, hogy Dürer "kezébe vett" egy hegyes romboédert, (hat egybevágó rombuszból álló, szerkezetét tekintve kocka-szerű poliédert), amelynek a két hegyesszögű testszögletét levágta két szabályos háromszöggel. A vita tárgya az, hogy milyen volt a csonkolás előtti romboéder, (pl. mekkorák a rombuszok szögei, vagy a rombuszok átlóinak az aránya), és "hol vágta el" a rombuszokat, vagyis mekkorák a levágott háromszögek oldalai az eredeti rombusz oldalaihoz képest. Ezt a kérdést mi most hagyjuk nyitva.Talán közismertnek tekinthető a kockának az a tulajdonsága, hogy a testátlóik, mint tengelyek körül 120°-os forgatással önmagába vihető. Egy nem derékszögű romboédernek -így a Dürer poliédernek is - csak egy ilyen tengelye van. Már csak ezért is érdemes a kockát "csúcsára állítani", mert könnyebben eligazodhatunk, ha ez a forgástengely a koordinátarendszer z tengelye.
Egy ilyen speciális helyzetben felvett (z forgástengelyű, origó középpontú) romboéder egyértelműen megadható pl. egy z-re nem illeszkedő csúcsával, így a Dürer-szerkezetű csonkolt romboéder megadásához elegendő három változtatható paramétert megadnunk.
Mi lenne, ha ...
A Dürer-poliédernek minden csúcsába három-három él fut be, van két háromszög és hat ötszöglapja.
Gondolhatnánk, hogy a poliéderen belül "ott van" egy (nem szabályos) oktaéder, amelynek két szemközti lapja a Dürer-poliéder két háromszöglapja.
Mi lenne, ha ... elvennénk ezeket a háromszöglapokat, helyettük az oktaéder további hat lapja alkotná az immár tórusz-szerű "lyukas" poliéder felület "belső" részét?
Önduális poliédereket keresve egyszeriben stimmelne a leltár: ennek a poliédernek hat ötszög és hat háromszöglapja lenne, és hat csúcsába öt-öt él, a másik hatba három-három él futna be. A házi szóhasználatunkkal élve: klónozható! Alkalmas méretezéssel talán elérhető, hogy a poliéder egybevágó legyen aduálisábal. Talán az is megoldható, hogy az ötszöglapok kerüljenek belülre, és a háromszöglapok kívülre. Így egy "Dürer-szerű" poliéder folytonos deformálással átmehet "oktaéderszerűbe".
Hátha valamelyik elrendezéssel önduális változatot is kaphatunk.
A fenti appletben a Dürer-poliéder alakját csúszkával szabályozott paraméterekkel adtuk meg, azt is megengedve, hogy a romboéder kockává sőt tompaszögűvé - lapos romboéderré - fajuljon. Ugyanígy a csonkolás helye, mértéke is változtatható. (Érdemes megjegyezni, hogy ugyanazokból a - nem túl hegyes - rombuszokból felépíthető egy hegyes és egy lapos romboéder is.
Az így kapott két - azonos szerkezetű - poliéder egymás duálisa. A Láthatóságuk az előző appletnél megismert módon szabályozható, formájuk a három csúszkával alakítható.
Van még az appletben három ikon-szerű rajz. Ezere kattintva a csúszkák felvesznek egy-egy speciális helyzetet, talán éppen azokat, amiket keresünk. Aki teheti, ezeket csak végszükség esetén használja, ne fossza meg magát az önálló felfedezés örömétől.
Ugyanis ezekkel a paraméterekkel nem csak kocka, a duálisával egybevágó "klón" hanem a klónjával egybe is eső változat is "kitapogatható".
Némi számolás árán az is belátható, hogy az így kapott változatok nem csak körül-belül, hanem matematikailag pontosan olyanok, amilyeneket kerestünk.
Ezzel matematikai szempontból is figyelemre méltó, különleges poliédert találtunk.Örülhetünk neki.
Csakhogy...
... csakhogy valójában nem így történt.
E sorok írójának Böszörményi István szobrászművész mutatott egy kockából kialakított "kívül-belül kockasíkok" változatot. Ebből kiindulva némi kísérletezés, számolgatás árán állt elő az a változat, amelyhez van olyan gömb, amelyre vonatkozó polaritás a poliédert pontosan önmagába viszi.
Ezt kerestük. Erről (is) készített térplasztikát a művész. Így hát ez a poliéder, vagy ez a műalkotás elmondhatná magáról, hogy "Én a klónom vagyok!" (Szerencsére a poliéderek épp úgy mint a szobrok eléggé hallgatagok.)
Vajon a matematika, vagy a képzőművészet szépsége - jószerével mindkettő - hatott-e jobban kedves olvasóinkra? Önökre bízzuk a választ.
Reméljük olvasóink is csatlakoznak ahhoz, hogy - így, együtt - fűzzünk hozzá két szót Orosz István fenti mottójához, miszerint ... "Ez nagyon érdekel."... minket is!