Cambiare il periodo dell'andamento
DESCRIVERE CAMBIAMENTI CON PERIODO QUALSIASI
Gli esempi di andamento esponenziale che abbiamo considerato finora erano caratterizzati da una variazione relativa costante per ogni variazione unitaria della variabile indipendente - per esempio una banca che garantisce un interesse del 2% annuo.
I fenomeni che ci capiterà di descrivere, tuttavia, potrebbero avere un periodo di cambiamento diverso. Come fare, ad esempio a riprodurre la seguente situazione?
ESEMPIO 1: Melissa ha un allevamento di 35 conigli, ed ogni 15 mesi il loro numero raddoppia
Possiamo facilmente individuare il valore di partenza, , ed il fattore di cambiamento, , dato che i conigli devono raddoppiare. Come rendere conto del fatto che questa variazione avviene ogni mesi?
Per quello che abbiamo imparato sulla funzione esponenziale, i conigli raddoppiano ogni volta che l'esponente aumenta di uno, perché questo implica che il valore iniziale sarà moltiplicato per un volta di più. Di conseguenza l'esponente della nostra funzione deve aumentare di uno ogni volta che passano mesi, o detta in altri termini deve contare quanti periodi da mesi sono passati. È abbastanza semplice verificare che la funzione cercata avrà forma
Puoi facilmente verificare infatti che l'esponente conta quanti " mesi" sono passati, e quindi restituisce i numero di "raddoppi" che i conigli hanno avuto nel frattempo. Ad esempio dopo 45 mesi abbiamo:
cioè i conigli, essendo trascorsi periodi di mesi, sono raddoppiati 3 volte.
Vediamo un altro esempio.
ESEMPIO 2: Se deposito i miei risparmi presso una banca mi offre le condizioni descritte dalla seguente funzione:
dove è il capitale iniziale che deposito in banca e è il capitale che mi viene restituito dopo anni. Quali sono le condizioni offerte dalla banca?
Il fattore di cambiamento è quindi la banca mi offre un interesse dello . Ogni quanto tempo mi viene corrisposto? Osservando l'esponente noto che dopo un anno ottengo
Cioè in un anno il mio capitale è aumentato dello due volte- si tratta in effetti della situazione speculare a quella vista nel primo esempio. Ne consegue che la banca di corrisponde un interesse dello due volte all'anno, cioè ogni semestre.
CALCOLARE IL TASSO RISPETTO AD UN PERIODO DIVERSO USANDO LE PROPRIETÀ DELLE POTENZE
Abbiamo visto che modificando l'espressione dell'esponente possiamo modulare il periodo con cui avviene la variazione relativa costante prevista dall'andamento esponenziale. Ora vedremo che manipolando l'esponente attraverso le proprietà delle potenze possiamo ottenere altre informazioni interessanti.
Riprendiamo l'esempio appena visto: mi interessa capire a quale interesse ANNUALE corrispondano le condizioni offerte dalla banca. Innanzitutto dobbiamo capire se ha senso porsi questa domanda - cioè la banca nella situazione descritta il mio capitale cambia ogni anno sempre della stessa percentuale? E se sì, quanto vale questa percentuale?
[Ci chiediamo anche: dato che in un anno ci sono due semestri, prenderò il 4%, cioè due volte il 2%?]
Se vogliamo ottenere un andamento che abbia periodo annuale, dovremo avere una potenza il cui esponente aumenta di uno ogni volta che passa un anno, cioè in cui compare solo . Possiamo ottenerla manipolando la funzione con le proprietà delle potenze, ed in particolare con l'inversa della proprietà di potenza di potenza:
calcolando la parte in rosso otteniamo
Leggendo la nuova forma ottenuta deduciamo che la banca ci garantisce l'interesse del annuo. Da notare che è un po' più del , cioè di due volte il , perché il secondo semestre prendo il su un capitale che contiene gli interessi del primo semestre, e quindi è un po' maggiore.
Vediamo ora come con questa stessa tecnica sia possibile scegliere un'unità di misura differente per il periodo di cambiamento, e calcolare il fattore relativo.
ESEMPIO 3: La popolazione di rinoceronti bianchi dimezza ogni anno. Qual è il suo tasso di riduzione MENSILE?
Se chiamiamo il numero di rinoceronti bianchi in questo momento, cioè il valore iniziale, otteniamo un dimezzamento all'anno con una funzione del tipo
Poiché siamo interessati alla variazione mensile, dobbiamo riformulare l'andamento in termini di mesi. Affermare che i rinoceronti dimezzano "ogni anno" equivale a dire, in termini di mesi, che dimezzano "ogni dodici mesi", di conseguenza l'esponente della nuova funzione dovrà "contare" i periodi di 12 mesi trascorsi
A questo punto per ottenere il fattore di cambiamento mensile dobbiamo isolare il termine all'esterno in modo che compaia una potenza che conti il numero di mesi trascorsi. Lo otteniamo tramite la proprietà di potenza di potenza, come abbiamo fatto nell'esempio precedente:
Calcoliamo ed otteniamo quindi
la funzione ottenuta afferma che ogni mese sopravvive (attenzione!) solo il dei rinoceronti presenti, quindi i rinoceronti diminuiscono del al mese.
NOTA: Anche in questo caso notiamo che il nuovo fattore di variazione NON si ottiene semplicemente moltiplicando o dividendo per il rapporto tra i due periodi. In altre parole anche se la variazione è del 50% annuo ed in un anno ci sono 12 mesi, la variazione mensile NON è . In questo caso la variazione mensile corretta è maggiore, perché ogni mese il numero di rinoceronti totale su cui viene calcolata la percentuale di animali che muoiono diminuisce, e di conseguenza diminuisce il numero di animali morti. Per compensare questo effetto e poter "eliminare" tutti i rinoceronti previsti dal tasso del 50% annuale è quindi necessario partire da una percentuale mensile più alta. puoi verificare questo effetto nella tabella riportata sotto, in cui si vede che il numero di rinoceronti morti ogni mese diminuisce, perché è il 6% di un numero sempre più piccolo.
Trovi altri esempi e spiegazioni nella seconda parte di questa playlist, i cui video parlano del calcolo di un tasso di variazione associato ad un periodo differente
https://youtube.com/playlist?list=PLgx1BjJWJCWs4PBep1kpgLEGQC0w3GSjU
UN'APPLICAZIONE: PROBLEMI DA DATI EMPIRICI
Quanto abbiamo visto finora ci dice anche che l'andamento esponenziale non è legato ad un determinato intervallo di tempo: se una grandezza ha una variazione relativa costante con una certa periodicità (ad esempio dimezza ogni anno, nell'esempio 3) avrà questo tipo di andamento (una variazione relativa costante) non solo per quel periodo (l'anno, nell'esempio) ma rispetto a qualsiasi intervallo di tempo; ovviamente la variazione associata al nuovo periodo cambierà: nell'esempio abbiamo trovato che anche ogni mese la variazione relativa è costante, in particolare ogni mese il numero di rinoceronti diminuisce .
Questo ci permette di affrontare dei problemi partendo da delle informazioni più flessibili, come vediamo nel seguente esempio.
ESEMPIO 4: una popolazione di stambecchi che tre anni fa era di 140 individui ne conta attualmente 119. Ipotizzando un andamento di tipo esponenziale, calcola quando vi saranno meno di 100 stambecchi (arrotonda al mese).
Il problema ci dice che in tre anni gli stambecchi sono diminuiti e ci fornisce la popolazione nei due momenti. Questi due dati da soli non possono dirci niente di come si comporta la popolazione: ad esempio potremmo anche pensare che sia costante la variazione assoluta, cioè che ogni 3 anni muoiano stambecchi, ma il problema stesso ci dice di assumere un andamento esponenziale (perchè è quello seguito spesso dalle popolazioni di individui) e quindi di assumere che sia costante la variazione relativa. Troviamo allora che in tre anni il numero di stambecchi è stato moltiplicato per , cioè che è sopravvissuto l' degli stambecchi. Cioè che ne sono morti il
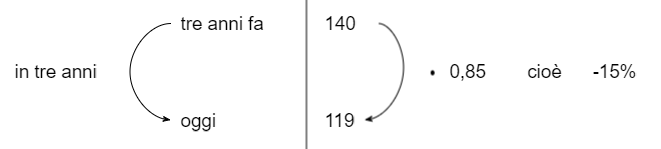
Dato che l'andamento esponenziale, quindi la variazione relativa è costante (sempre la stessa), se in tre anni vi è stata una diminuzione del possiamo assumere che questa variazione si ripeta ogni volta che passano tre anni, cioè possiamo assumere che il numero di stambecchi diminuisca del ogni tre anni. La popolazione avrà quindi un andamento del tipo
ATTENZIONE: per come abbiamo costruito la funzione è la popolazione che risulta quando sostituiamo al posto di , quindi la popolazione presente adesso: dal problema vediamo che adesso vi sono stambecchi quindi la funzione completa è:
[possiamo verificare che se consideriamo la popolazione di tre anni fa, cioè , sostituendo e svolgendo i calcoli otteniamo i stambecchi previsti]
Siamo pronti a rispondere alla domanda. Per trovare quando ci saranno stambecchi impostando
che risolta ci dà cioè fra circa 3 anni e due mesi e mezzo. Dato che la popolazione sta diminuendo, vi saranno almeno 100 stambecchi PRIMA di questa scadenza, ed in particolare fino a 3 anni e due mesi, dato che dovevamo arrotondare ai mesi, mentre dopo ve ne saranno di meno.
NOTA: avremmo potuto costruire la funzione anche in modo diverso, usando come dato di riferimento i stambecchi, sarebbe però stato necessario ricordare che è il dato relativo a tre anni fa. Riscriviamo allora la nostra funzione modello in questo modo:
Notiamo che adesso abbiamo costruito l'esponente in modo che si azzeri (e quindi l'intera funzione restituisca ) quando , quindi il valore di riferimento deve essere il numero presente tre anni fa. Possiamo quindi inserire il dato nella funzione
Puoi verificare che se calcolo (gli stambecchi oggi) ottengo correttamente e che anche la domanda del problema fornisce la stessa risposta.
Trovi ulteriori esempi ed approfondimenti su questo argomento in questa playlist:
https://youtube.com/playlist?list=PLgx1BjJWJCWsefxFqPkNXKwVAcXZ1Vzq3