Funzioni goniometriche seno e coseno
Hai già incontrato seno e coseno (e forse anche tangente) in Fisica, cosa ti ricordi?
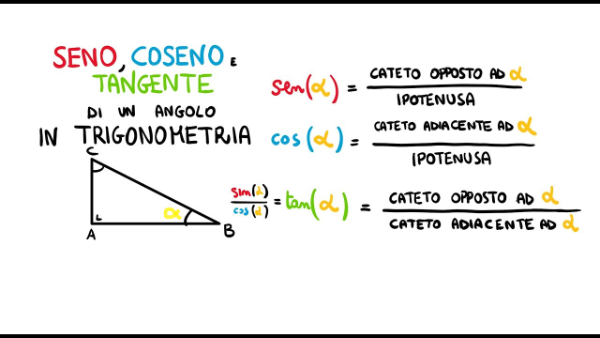
Il seno e il coseno (e la tangente) sono funzioni che associano a un angolo un valore numerico. Si definiscono in un triangolo rettangolo con le formule seguenti:
Questa è la CIRCONFERENZA GONIOMETRICA, cioè la circonferenza di centro l'origine e raggio 1. La useremo moltissimo per leggere seno e coseno degli angoli.
Qual è l'equazione della circonferenza goniometrica?
Sulla circonferenza gli angoli si leggono percorrendola in senso antiorario a partire dal punto (1,0) che corrisponde all'angolo di 0°. Prima di agire sullo slider, prova a rispondere alle seguenti domande. a) Quali sono le coordinate del punto della circonferenza che corrisponde a 90°? b) Quale angolo corrisponde al punto (-1,0)? c) Quale angolo corrisponde al punto (0,-1)? d) Quali sono le coordinate del punto della circonferenza che corrisponde a 360°? e) In quale quadrante si hanno gli angoli acuti? f) In quali quadranti si hanno gli angoli concavi? Esplora l'ampiezza dell'angolo muovendo lo slider e trova conferma delle tue risposte.
Ora nella finestra GeoGebra di sopra esplora con lo slider il calcolo di seno e coseno di ciascuno angolo: fai riferimento alle formule di sopra relative al triangolo rettangolo! a) Dove leggi il coseno e il seno di un angolo sulla circonferenza goniometrica? b) Tra quali valori sono compresi il seno e il coseno di un angolo? c) In quali quadranti il seno è positivo? In quali quadranti il coseno è positivo? e) Qual è la relazione che lega il seno e il coseno di un angolo (siccome ciascun angolo è associato a un punto della circonferenza goniometrica)? f) Quanti angoli della circonferenza goniometrica hanno il seno e il coseno uguali tra loro? Quali saranno i valori di seno e coseno in questi angoli? g) Dato un angolo acuto, qual è l'altro angolo della circonferenza che ha lo stesso seno? E lo stesso coseno? E seno e coseno rispettivamente opposti?