Objeto de Aprendizagem - LEM2 - Bruno do Vale
Objeto de aprendizagem digital para o Ensino/Aprendizagem de Matemática (OA)
Motivação
Questão 01
Você consegue pensar em exemplos do seu cotidiano em que você visualiza um lançamento oblíquo? Descreva-os no espaço abaixo.
Questão 02
Você consegue lembrar a equação que rege a posição no movimento retilíneo uniforme? Caso não recorde, utilize o gráfico abaixo da questão para guiá-lo. Lembre-se que, em um gráfico que relaciona a velocidade com o tempo, a área sobre a curva representa o deslocamento da partícula!
Gráfico v x t do movimento retilíneo uniforme
Questão 03
Você consegue lembrar a equação que rege a posição no movimento retilíneo uniformemente variado? Caso não recorde, utilize o gráfico abaixo da questão para guiá-lo. Lembre-se que, em um gráfico que relaciona a velocidade com o tempo, a área sobre a curva representa o deslocamento da partícula!
Gráfico v x t do movimento retilíneo uniformemente variado
Questão 04
Agora que relembramos as equações para cada um dos movimentos que utilizaremos, precisamos ver como decompor o vetor velocidade! Conhecendo a magnitude do vetor velocidade e o ângulo que ele forma com o eixo horizontal, quais as componentes horizontal (utilizaremos subíndice x) e vertical (utilizaremos subíndice y) da velocidade? Novamente, faça usufruto do gráfico abaixo da questão para auxiliá-lo. Aproveite para brincar com os valores da velocidade e do ângulo!
Vetor Velocidade
Desenvolvimento da fórmula
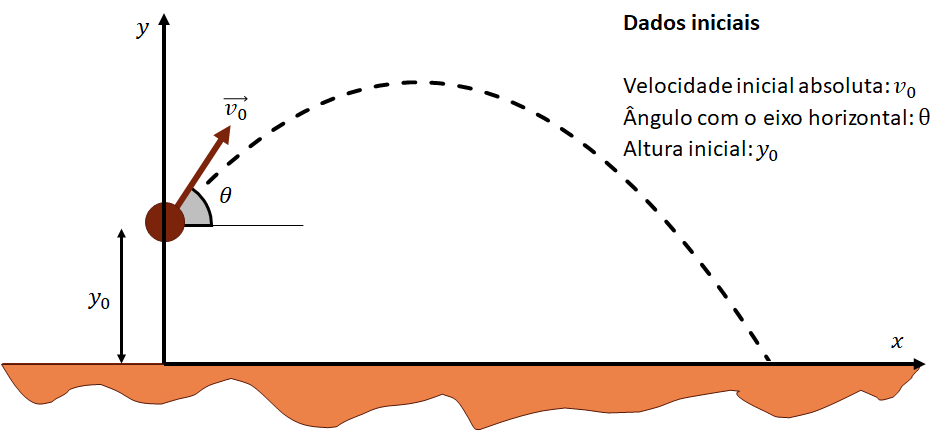
Questão 05
Quais informações do lançamento você conseguiria extrair da fórmula da parábola? Para auxiliá-los, vamos visualizar a fórmula obtida para a parábola no Geogebra logo abaixo. Altere os valores dos dados iniciais no gráfico abaixo e veja como esses afetam o lançamento! Além disso, não se esqueça que 100 m/s = 360 km/h. Ou seja, já é um valor substancial! A velocidade do som, por exemplo, com uma temperatura de 20ºC, é de aproximadamente 343 m/s. De qualquer modo, seja criativo na escolha dos dados iniciais! =D Obs.: As curiosidades são algumas das possíveis respostas para esta questão, mas não são as únicas!
Questão 06
No desenvolvimento do programa, decidimos por escolher como aceleração da gravidade o valor g=9,81 m/s^2, o que já é uma aproximação. Em seus exercícios, contudo, verão que é muito comum arredondá-la para 10 m/s^2. Poderíamos nos perguntar: quais os efeitos disso nos resultados? E é por isso que deixamos a aceleração da gravidade em aberto! Escolha alguns valores para os dados iniciais e veja a altura máxima e o alcance máximo para os dois valores de gravidade. Indiquem na resposta tanto os valores escolhidos quanto os valores obtidos. O que vocês acharam dos resultados? Acreditam que a diferença seja significativa? Brinquem um pouco mais. Pesquise o valor da gravidade na Lua, e veja como será a trajetória! Vocês acham que as condições que estabelecemos pro movimento também se aplicariam lá?
Questão 07
Agora é com vocês! Com base no conteúdo exposto e no material à disposição nesta atividade, crie uma pergunta a respeito ou lance um questionamento/feedback que você acha pertinente de ser abordado.