Matrix Drehung um AchsenGerade durch Ursprung R³
Konstruktion der Drehung und Ableitung der Drehmatrix
Algebra Fenster:
Achsenvektor v
Drehwinkel w
Drehe um Achse v mit Winkel w
Drehkreismittelpunkt e_k: , k=x,y,z
Drehkreismittelpunkt P: M_p:=v ((v P) / v²)
Die Bildvektoren e' bilden die Drehmatrix
Wickipedia:
v= = (n1,n2,n3).
mit
R(w) stellt die ermittelten e' dar
und
R_w stellt das Ergebnis mittels der (wikipedia) Formel dar:
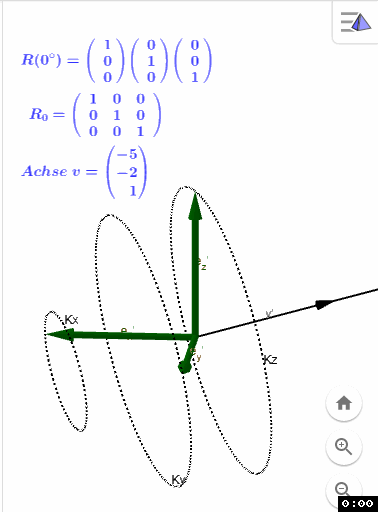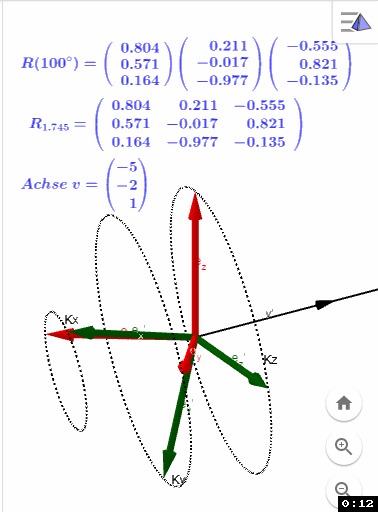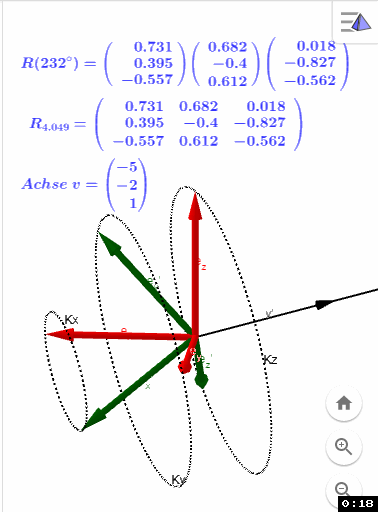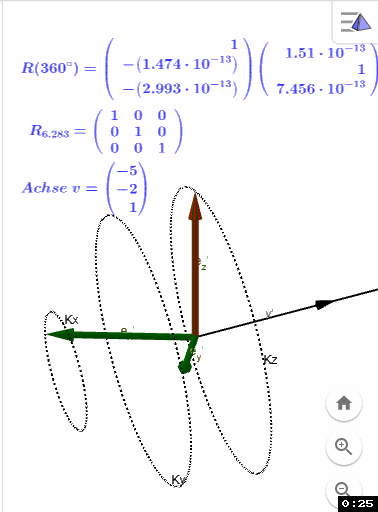
DrehungAchsenGeradeDrehKreis.ggb
o=x,y,z, e_o Vektor Standardbasis, Achsenvektor v=(n1,n2,n3), Drehwinkel t (w)
E_o Ebene mit Richtungsvektor der Achsengeraden v als Normalenvektor durch e_o
E_o: v((x,y,z)-e_o)=0
Drehkreismittelpunkt D_o: Schnittpunkt Achsengerade t v E_o für
v (t v - e_o)=0 ===> t= v e_o/ v^2 ===> D_o=(v e_o/ v^2) v
D_o=(n1,n2,n3) e_o/(n1,n2,n3)^2 * (n1,n2,n3)
Konstruiere einen Vektor (x,y,z)=u (e_o-D_o)
(e_o - D_o) (x,y,z)=0
für einen Kreis in Ebene E_o (u E_o)
(n1,n2,n3) ((x, y, z) - D_o),
mit dem Radius (e_o-D_o)
((x,y,z)-D_o)^2=(e_o - D_o)^2 }
Löse GLS:
Drehkreis:
D_x(n1,n2,n3) + ((u_x(n1,n2,n3)-D_x(n1,n2,n3)) sin(t)+ (e_x-D_x(n1,n2,n3))cos(t))
D_y(n1,n2,n3) + ((u_y(n1,n2,n3)-D_y(n1,n2,n3)) sin(t)+ (e_y-D_y(n1,n2,n3))cos(t))
D_z(n1,n2,n3) + ((u_z(n1,n2,n3)-D_z(n1,n2,n3)) sin(t)+ (e_z-D_z(n1,n2,n3))cos(t))
für n12+n22+n32 = 1 ergibt {e'_x, e'_y, e'_z} = R(,n1,n2,n3)
Formula
Wickipedia:
R(a,n1,n2,n3)
{{n1^2*(1 - cos(a)) + cos(a), n1*n2*(1 - cos(a)) - n3*sin(a), n1*n3*(1 - cos(a)) + n2*sin(a)},
{n2*n1*(1 - cos(a)) + n3*sin(a), n2^2*(1 - cos(a)) + cos(a), n2*n3*(1 - cos(a)) - n1*sin(a)},
{n3*n1*(1 - cos(a)) - n2*sin(a), n3*n2*(1 - cos(a)) + n1*sin(a), n3^2*(1 - cos(a)) + cos(a)}}
$7: Formelkonstruktor
D_x(n1, n2, n3) + (u_x(n1, n2, n3) - D_x(n1, n2, n3)) sin(t) + (e_x - D_x(n1, n2, n3)) cos(t)
Drehmatrix R für Achsenvektor v=(n1,n2,n3) und Winkel t
{
{(n1^2*(1-cos(t))+(n1^2+n2^2+n3^2)*cos(t)), (n1*n2*(1-cos(t))-n3*sin(t)*sqrt(n1^2+n2^2+n3^2)), (n2*n3*(1-cos(t))-n1*sin(t)*sqrt(n1^2+n2^2+n3^2))},
{(n1*n2*(1-cos(t))+n3*sin(t)*sqrt(n1^2+n2^2+n3^2)), (n2^2*(1-cos(t))+(n1^2+n2^2+n3^2)*cos(t)), (n2*n3*(1-cos(t))-n1*sin(t)*sqrt(n1^2+n2^2+n3^2))},
{(n1*n3*(1-cos(t))-n2*sin(t)*sqrt(n1^2+n2^2+n3^2)), (n2*n3*(1-cos(t))+n1*sin(t)*sqrt(n1^2+n2^2+n3^2)), (n3^2*(1-cos(t)))+(n1^2+n2^2+n3^2)*cos(t)}
}*1/(n1^2+n2^2+n3^2)
n1^2+n2^2+n3^2=1
[/size]
| (n1^2*(1-cos(t))+cos(t)) | ((n1*n2*(1-cos(t))-n3*sin(t)) | (n1*n3*(1-cos(t))+n2*sin(t)) |
| ( n1*n2*(1- cos(t))+n3*sin(t)) | (n2^2*(1-cos(t))+cos(t)) | (n2*n3*(1-cos(t))-n1*sin(t)) |
| (n1*n3*(1- cos(t))-n2*sin(t)) | (n2*n3*(1-cos(t))+n1*sin(t)) | (n3^2*(1-cos(t)))+cos(t) |
Matrizen für Drehungen und Spiegelungen in GeoGebra CAS
Exkurs (vollständigkeitshalber)
Drehungen um Koordinatenachsen
Do(χ,a):=Take({{ (1, cos(a),cos(a))χ, (0,0,-sin(a))χ ,(0, sin(a), 0)χ}, {(0,0, sin(a))χ, ( cos(a) ,1, cos(a) )χ, (-sin(a),0,0)χ}, {(0,-sin(a),0)χ, (sin(a),0,0)χ, (cos(a) , cos(a) ,1)χ }} ,1,3)
Dz(a)=Do((0,0,1),a)
Spiegelung
n=(n1,n2,n3) normierter Achsenvektor (Ursprungsgerade g(t):=t v, v=(1,1,1)/sqrt(3), )
S_n(n1,n2,n3):=Take({{2n1² - 1, 2n1 n2 , 2n1 n3 }, {2n1 n2 , 2n2² - 1, 2n2 n3 }, {2n1 n3 , 2n2 n3 , 2n3² - 1}},1,3)
S_v:=S_n(x(v),y(v),z(v))
ov Ortsvektor, rv Richtungsvektor der Spiegel-Geraden g
GS(po,oo,ro):=2 (oo+(Dot(po-oo,ro))/(Dot(ro,ro))*ro)-po
Ursprungs-Ebene Normalenvektor no=(n1,n2,n3)
SP(no,vo):=vo-2Dot(vo,no)/Dot(no,no)*no
S_N(n1,n2,n3):=Take({{((-n1^(2)) + n2^(2) + n3^(2)) / (n1^(2) + n2^(2) + n3^(2)), (((-2) * n1) * n2 / (n1^(2) + n2^(2) + n3^(2))), (((-2) * n1) * n3 / (n1^(2) + n3^(2) + n2^(2)))}, {(((-2) * n2) * n1 / (n2^(2) + n1^(2) + n3^(2))), ((-n2^(2)) + n1^(2) + n3^(2)) / (n2^(2) + n1^(2) + n3^(2)), (((-2) * n2) * n3 / (n2^(2) + n3^(2) + n1^(2)))}, {(((-2) * n3) * n1 / (n3^(2) + n1^(2) + n2^(2))), (((-2) * n3) * n2 / (n3^(2) + n2^(2) + n1^(2))), ((-n3^(2)) + n1^(2) + n2^(2)) / (n3^(2) + n1^(2) + n2^(2))}},1,3)
mit
Sn:=S_N(x(v),y(v),z(v))
Beliebige Ebene E:=no ((x,y,z)-p)=0, R Urbild, R' Bild
d:=no p (Abstand Ebene vom Ursprung)
R'=Sn (R-no p) + no p
