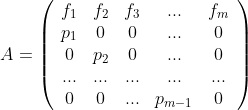Matrices de Leslie
MODELO POBLACIONAL DE LESLIE
Supongamos que estamos estudiando una población que se puede dividir en grupos de edades disjuntas: Grupo 1 [0; L) / Grupo 2 [L; 2L) / Grupo 3 [2L; 3L) / Grupo 4 [3L; 4L) ....... / Grupo m [(m-1)L; mL) Cada grupo (o clase) constituye un rango de L unidades de tiempo y se supone que la vida media de un individuo de esta población es de mL unidades de tiempo. Normalmente cuando se habla de modelos de Leslie para poblaciones estructuradas por edades, se hace referencia al número de hembras, entendiendo que se conoce la dinámica de la población en función del número de hembras de la misma. Los recuentos se hacen cada L unidades de tiempo. Para determinar el número de individuos en un instante de observación posterior se tienen en cuenta dos parámetros: tasa de fertilidad de las hembras y probabilidad de supervivencia. Denotaremos por fi con i=1,...., m, al número medio de crías hembras que tiene una hembra del grupo i-ésimo en ese periodo. Denotamos por pi con a la probabilidad de que una hembra del grupo i-ésimo esté viva en el siguiente recuento (que forme parte del grupo i + 1). Denotamos por el vector que recoge la cantidad de hembras, por sectores, en el momento n. Así podemos escribir el sistema de ecuaciones en diferencias:
que signi fica que la población en el instante n + 1 se obtiene de la población en el instante n mediante la matriz de Leslie que puedes ver abajo. Una matriz de Leslie tiene un único valor propio positivo () Este valor propio tiene multiplicidad 1 y el vector propio asociado V1 tiene todas sus componentes positivas. Además:- Si < 1 la población se extingue.
- Si > 1 la población crece exponencialmente, con razón geométrica .
- Si = 1 la población tiende al equilibrio .