Lineare Funktionen (Geraden)
Dieser Abschnitt beschäftigt sich mit den linearen Funktionen, die alle durch Funktionsgleichungen beschrieben werden können.
Es gibt folgende lineare gerade Funktionen:
- Hauptform
- Punkt-Steigungsform
- Zwei-Punkte-Form
- Berechnung im Koordinatensystem
In der App siehst du eine Funktion mit der Gleichung Mit dem Regler bei m kannst du die Steigung der Geraden verändern.
Der Regler c ändert dir den Schnittpunkt der Geraden mit der y-Achse, den sogenannten y-Achsenabschnitt c. Die blau gestrichelte Linie zeigt dir dabei an, wie weit der Schnittpunkt vom Nullpunkt der Achsen entfernt liegt.
Wie du schon bemerkt hast, ist auch eine Tabelle dargestellt. Diese verändert ihre Werte sofort, sobald du die Regler bewegst.
Die Punkte P1 und P2 sind absichtlich beweglich eingebettet. Verschiebe sie mal und beobachte, wie sich das Verhältnis ändert. Kleiner Hinweis: im Bruch werden die Verhältnisse immer als kleinstmöglicher ganzzahliger Bruch dargestellt.
parallele und senkrechte Geraden
Wenn du parallele bzw. senkrechte Geraden zu einer Funktionsgleichung wissen möchtest, dann gibt es da einfache Tricks.
parallele Gerade: jede Gerade, welche dieselbe Steigung hat wie die Gerade der ursprünglichen Funktion, ist parallel, sie unterscheiden sich nur im y-Achsenabschnitt.
senkrechte Gerade: jede Gerade, deren Steigung der negative Kehrwert der Geraden der ursprünglichen Funktion ist, verläuft senkrecht zu ihr.
Schau dir dazu einfach die Beispiele hier an.
Der blaue Punkt kann bewegt werden. Durch die "Drehung am Ursprung" werden die Gerade, das Steigungsdreieck sowie die x- und y-Achse um 90° gedreht. Dadurch wird die Steigung der senkrechten Gerade ersichtlich.
Hauptform
Die Hauptform der Funktionsgleichungen einer linearen Funktion lautet: oder
f(x) bedeutet: Funktion von x (damit wird errechnet, welcher y-Wert für ein beliebiges x vorliegt, daher ist f(x) und y gelichwertig zu betrachten)
m gibt die Steigung einer Geraden im Koordinatensystem an. Je größer m ist, desto steiler steigt oder fällt die Gerade. Ob eine Gerade fällt oder steigt, sieht man am Vorzeichen von m: + bedeutet steigen, - bedeutet fallen. m kann durch ein Steigungsdreieck bestimmt werden.
b gibt den so genannten y-Achsenabschnitt an, damit weiß man, an welcher Stelle die Gerade genau die y-Achse schneidet. Der x-Wert der Geraden ist an dieser Stelle immer gleich 0.
x0 ist die Stelle, an der die Gerade die x-Achse schneidet, der y-Wert ist dabei immer gleich 0.
![[size=85]In der App siehst du eine Funktion mit der Gleichung [math]y=m⋅x+c[/math]
Mit dem Regler bei m kannst du die Steigung der Geraden verändern.
Der Regler c ändert dir den Schnittpunkt der Geraden mit der y-Achse, den sogenannten y-Achsenabschnitt c. Die blau gestrichelte Linie zeigt dir dabei an, wie weit der Schnittpunkt vom Nullpunkt der Achsen entfernt liegt.[/size]](https://www.geogebra.org/resource/uefyraws/1LtgfiOZPbBC0aXc/material-uefyraws.png)
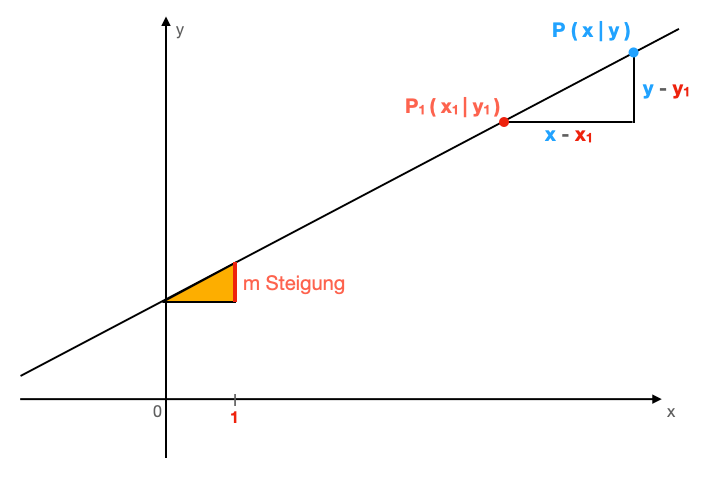
Punkt-Steigungsform
Wenn man die Steigung einer linearen Funktion direkt bestimmen möchte, wendet man am einfachsten die Punkt-Steigungs-Form an:
Umgestellt nach y ergibt sich folgende Gleichung:
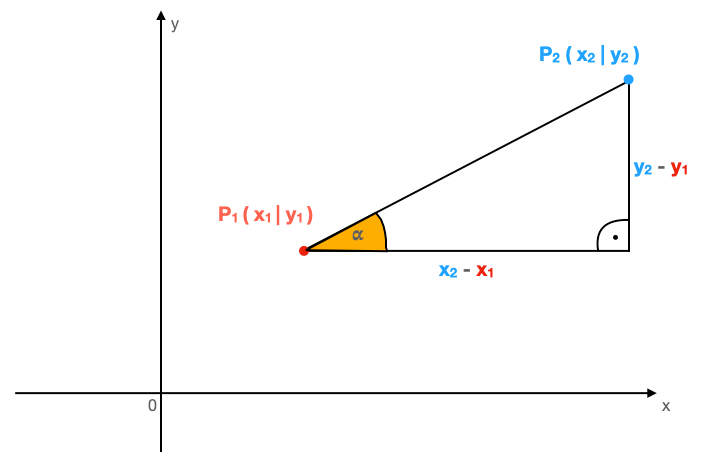
Zwei-Punkte-Form
Hier findest du die Formeln für die Zwei-Punkte-Form:
bzw.
Zwei-Punkte-Form
Berechnung im Koordinatensystem
Möchte man die Länge einer Strecke bestimmen, dann verwendet man diese Form: