Διαστημόμετρο ή παχύμετρο
Το κλασσικό παχύμετρο, είναι το απλό παχύμετρο vernier (ή βερνιέρος όπως συνηθίζεται
να λέγεται στην Ελλάδα), το οποίο πήρε το όνομά του από τον Γάλλο μαθηματικό Vernier,
που ανακάλυψε την ομώνυμη κλίμακα, τον 16ο αιώνα.
Αυτό το παχύμετρο, έχει τη δυνατότητα να μετρήσει πάχος, διάμετρο και βάθος με αρκετή ακρίβεια.
Η ακρίβεια εξαρτάται από το πόσο καλό είναι το παχύμετρο. Συνήθως θα δείτε
ακρίβεια μέχρι και 0.05 του χιλιοστού (μικρότερη υποδιαίρεση 0,05 mm)
Μέρη σε παχύμετρο vernier
Ας ξεκινήσουμε πρώτα από τα μέρη τα οποία έχει ένα τέτοιο παχύμετρο.

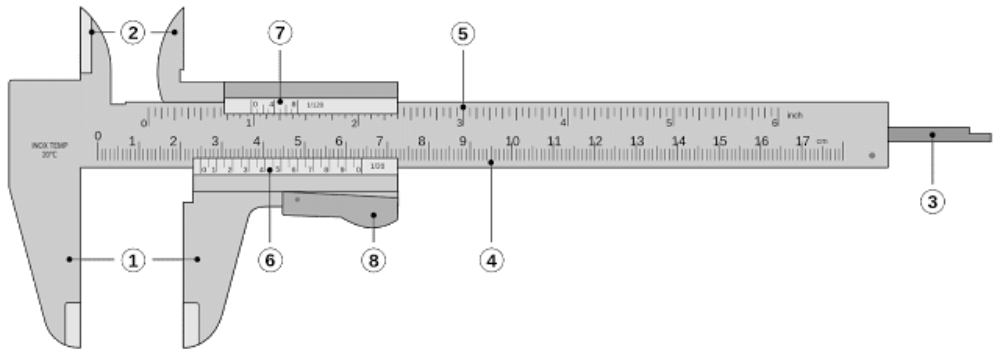
Αποτελείται από δύο τμήματα:
· το σταθερό τμήμα με δύο μεγάλες κύριες κλίμακες (4 σε cm & mm και 5 στο πάνω μέρος σε ίντσες).
Δίνει μια μέτρηση με ακρίβεια ενός δεκαδικού.
· το κινητό τμήμα με την κλίμακα του βερνιέρου ( 6 υποκλίμακα της κυρίας κλίμακας)
το οποίο ολισθαίνει πάνω στο σταθερό τμήμα. Μπορεί να δώσει μεγαλύτερη ακρίβεια δεκαδικού.
Ο βερνιέρος διαιρείται σε 10 ίσα διαστήματα και κάθε διαίρεση χωρίζεται σε 5 υποδιαιρέσεις και
επομένως ο συνολικός αριθμός των διαιρέσεων είναι 50.
Αν βιδώσεις την ασφάλεια (βίδα σύσφιξης) ή αν πιέσεις τον μοχλό (8), μπορείς να
εμποδίσεις αυτή τη μετακίνηση. Έτσι μπορείτε να κρατήσετε σταθερά τη μέτρηση την οποία κάνετε.
Στα τμήματα αυτά υπάρχουν οι σιαγόνες μέτρησης μεταξύ των οποίων τοποθετείται το σώμα
που θέλουμε να μετρήσουμε. Τα ζεύγη σιαγόνων μέτρησης, είναι δύο.
Ένα σετ για εξωτερικές μετρήσεις (1) ενώ το άλλο για εσωτερικές (2).
Οι σιαγόνες για εξωτερικές μετρήσεις έχουν 3 διαφορετικά μέρη. Στο πάνω μέρος έχουν ένα μικρό άνοιγμα. Το άνοιγμα αυτό είναι για να βοηθάει όταν υπάρχουν μικρά μέρη που δεν θέλετε να μετρήσετε.
Η μέτρηση θα πρέπει να γίνεται στο κύριο μέρος της σιαγόνας το οποίο ξεκινάει μετά το άνοιγμα.
Στο κύριο μέρος της σιαγόνας, το μέταλλο στο τέλος είναι αρκετά λεπτό. Ο λόγος είναι για να μπορείτε να μετράτε σπειρώματα.
Εκτός από τις σιαγόνες, έχει και μια κρυφή λάμα (βελόνα) στο πίσω μέρος,
το στέλεχος για μέτρηση βάθους μιας κοιλότητας (3).
Μετρήσεις
Με το παχύμετρο μπορούμε να μετρήσουμε:
1. το μήκος ενός αντικειμένου,
2. την εξωτερική και εσωτερική διάμετρο π.χ ενός σωλήνα,
3. το βάθος μιας οπής ή το βάθος των αυλακιών σε μια βίδα
Πώς μετρώ με το παχύμετρο
Κάθε υποδιαίρεση της κύριας κλίμακας είναι 1 mm, ενώ κάθε υποδιαίρεση του βερνιέρου είναι 0,05 mm.
· Τοποθετούμε το σώμα μεταξύ των κατάλληλων σιαγόνων (εσωτερική ή εξωτερική διάμετρο) ή
βυθίζουμε την βελόνα του στο εσωτερικό της κοιλότητας, το βάθος της οποίας θα μετρήσουμε.
· Μετακινούμε τον βερνιέρο, ώστε οι σιαγώνες να εφάπτονται απόλυτα στο σώμα.
Με την ειδική βίδα που βρίσκεται στο πάνω μέρος του βερνιέρου σταθεροποιούμε τις σιαγόνες και
έτσι μπορούμε να αφαιρέσουμε το προς μέτρηση σώμα.
· Ότι και να μετράτε (πάχος, διάμετρο ή βάθος) ο τρόπος που διαβάζετε την κλίμακα δεν αλλάζει.
Πρώτα πρέπει να δείτε την μεγάλη κλίμακα. Το μηδέν του βερνιέρου δείχνει πάνω στην
κύρια κλίμακα το ακέραιο κομμάτι της μέτρησης σε mm
(είναι ίσο με την απόσταση του μηδενός του βερνιέρου από το μηδέν της κυρίας κλίμακας).
Αυτή θα είναι η μέτρηση σας με ακρίβεια ενός χιλιοστού.
· Αν θέλετε περισσότερη ακρίβεια θα πρέπει να μετρήσετε και την μικρή κλίμακα Vernier.
Για να το κάνετε αυτό θα πρέπει να βρείτε:
σε ποιο σημείο η μικρή κλίμακα έρχεται σε απόλυτη αντιστοιχία με την μεγάλη. Δηλαδή,
την πρώτη γραμμή της μικρής κλίμακας που είναι στην ίδια ευθεία με μια γραμμή της μεγάλης.
- Η υποδιαίρεση του βερνιέρου που βρίσκεται στην ίδια ευθεία με κάποια υποδιαίρεση της κύριας κλίμακας, δίνει το δεκαδικό κομμάτι της μέτρησης. (Πολλαπλασιάζω τις υποδιαιρέσεις του βερνιέρου με 0,05 mm, που είναι η κάθε υποδιαίρεση.)
- Προσθέτω τα δύο κομμάτια, ακέραιο και δεκαδικό.
Παράδειγμα:

Στην Εικόνα το μηδέν του βερνιέρου δείχνει 69 mm (και κάτι ακόμα). Η 3 η υποδιαίρεση
του βερνιέρου βρίσκεται στην ίδια ευθεία με υποδιαίρεση της κύριας κλίμακας.
Άρα, το δεκαδικό κομμάτι είναι 3 x 0,05 mm=0,15 mm. Προσθέτοντας, έχω 69,15 mm.
Γραφή αποτελέσματος
Όπως ξέρουμε, μετρώντας ένα μέγεθος μία φορά, το αποτέλεσμα με σφάλμα το γράφω:
μέτρηση ± η μικρότερη υποδιαίρεση του οργάνου.
Στο παραπάνω παράδειγμα η μέτρηση είναι 69,15 mm. Η μικρότερη υποδιαίρεση του
παχύμετρου είναι 0,05 mm. Άρα, θα γράψω το αποτέλεσμα ως εξής: (69,15 ±0,05) mm .