Vectores
Introducción
En física, el entendimiento de los conceptos básicos relativos a este tipo de cantidades son fundamentales en la consecución de las metas de aprendizaje para algunos cursos de educación media y superior, ya que estos juegan un papel importante en las diferentes etapas del proceso educativo, facilitando el estudio y comprensión de una amplia variedad de fenómenos, entre los que sobresalen el movimiento y los campos. En este trabajo se analiza la incidencia de la aplicación de una secuencia didáctica que tiene por objetivo la solución de problemas sobre la representación y la suma vectorial por métodos gráficos (en los casos unidimensional y bidimensional), utilizando un software de geometría dinámica, GeoGebra.
Descripción General
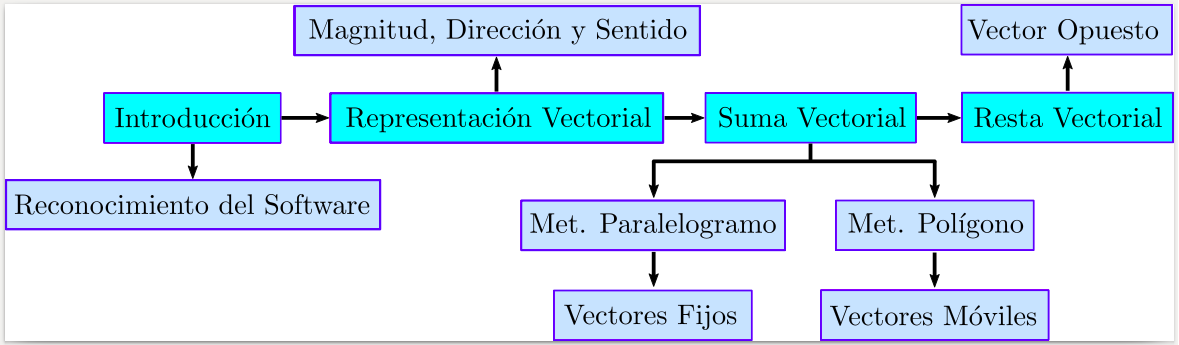
Resumen Teórico (Representación Vectorial)
Representación Vectorial (1D y 2D)
A continuación se presenta un applet a traves del cual, se representan dos vectores (A y B). En la representación se puede manipular la magnitud y dirección de cada vector.
Representación de Vectores (1D y 2D)
Resumen Teórico (Suma Vectorial)
Suma de Vectores por el Método del Paralelogramo
A continuación se presenta un applet a traves del cual, se suman dos vectores (A y B) mediante el método del paralelogramo. En la adición se puede manipular la magnitud y dirección de cada vector. Se presenta la magnitud y dirección del vector suma (S).
Suma de Vectores por el Método del Paralelogramo
Suma de Vectores por el Método del Polígono
A continuación se presenta un applet a traves del cual, se suman dos vectores (A y B) mediante el método del polígono. En la adición se puede manipular la magnitud y dirección de cada vector. Se presenta la magnitud y dirección del vector suma (S).
Suma de Vectores por el Método del Polígono
Resumen Teórico (Resta Vectorial)
Resta de Vectores por el Método del Paralelogramo
A continuación se presenta un applet a traves del cual, se restan dos vectores (A y B, se efectua la operación A - B, es importante aclarar esto, ya que la resta de vectores no es conmutativa) mediante el método del paralelogramo. Adicionalmente, se construye el vector opuesto de B, necesario para efectuar la resta. En la resta se puede manipular la magnitud y dirección de cada vector. Se presenta la magnitud y dirección del vector resta (R).
Resta de Vectores por el Método del Paralelogramo
Resta de Vectores por el Método del Polígono
A continuación se presenta un applet a traves del cual, se restan dos vectores (A y B, se efectua la operación A - B, es importante aclarar esto, ya que la resta de vectores no es conmutativa) mediante el método del polígono. Adicionalmente, se construye el vector opuesto de B, necesario para efectuar la resta. En la resta se puede manipular la magnitud y dirección de cada vector. Se presenta la magnitud y dirección del vector resta (R).


