Punkte im Raum: Das dreidimensionale Koordinatensystem
Um Standorte anzugeben brauchen Systeme die Hilfe der Mathematik. Dort werden Standorte als Koordinaten angegeben. Manchmal reichen hierfür zweidimensionale Koordinaten aus, aber in einigen Kontexten werden auch Raumkoordinaten mit drei Einträgen benötigt.
Ein Beispiel siehst du im Video.
Um Drohnenshows mit der benötigten Präzision zu koordinieren, muss jeder Drohne zu jedem Zeitpunkt eine genaue Position in der Luft zugewiesen werden. Unser bekanntes zweidimensionales Koordinatensystem reicht hierfür nicht aus.
Warum?
Information: Koordinaten im Raum (In deine Unterlagen übertragen!)
Um die Lage eines Punktes im Raum anzugeben, benötigen wir ein Koordinatensystem mit drei Achsen.
Dabei verläuft die x1-Achse nach vorne, die x2-Achse nach rechts und die x3-Achse nach oben.
Konvention: Im Heft entsprich eine Kästchendiagonale auf der x1-Achse einem Zentimeter.
Die Lage eines Punktes P im Raum werden als Zahlentripel P( | | ) angegeben.
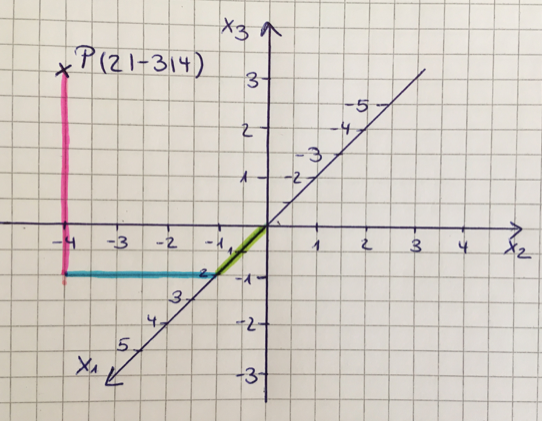
Aufgabe 1
Nutze die Visualisierung, um dir die Funktionsweise des dreidimensionalen Koordinatensystems zu verdeutlichen.
Aufgabe 2
Bearbeite die Aufgabe mindestens sechs mal richtig. Überprüfe deine Lösung.
Aufgabe 3
Welche Koordinaten könnten zum Punkt C gehören? Welches Problem ergibt sich?
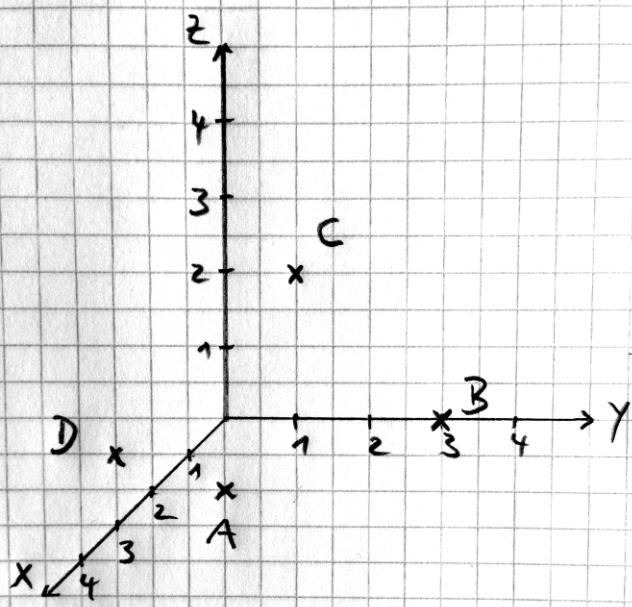
Aufgabe 4
Kreuze an, welche Punkte auf der x1-Achse liegen:
Kreuze an, welche Punkte auf der x2-Achse liegen:
Kreuze an, welche Punkte auf der x3-Achse liegen:
Erkläre in eigenen Worten, wie du erkennen kannst, ob ein Punkt auf einer Koordinatenachse liegt!
Information: Koordinatenebenen (in deine Unterlagen übertragen!)
Im dreidimensionalen Koordinatensystem spannen jeweils zwei Koordinatenachsen eine Koordinatenebene auf.
So entstehen drei Ebenen (x1x2-Ebene, x2x3-Ebene, x1x3-Ebene).
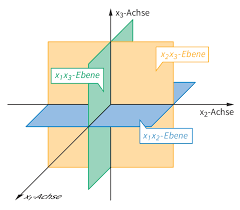
Aufgabe 5
Kreuze an, welche Punkte in der x1x2-Ebene liegen:
Kreuze an, welche Punkte in der x1x3-Ebene liegen:
Kreuze an, welche Punkte in der x2x3-Ebene liegen:
Aufgabe 6
Gibt die richtigen Koordinaten an. Lasse dir dann einen neuen Punkt anzeigen.
Bestimme insgesamt sechs Koodinaten.
Zusatzaufgabe
Der Punkt P(1|2|3) wird gespiegelt:
- an der x1x2-Ebene
- an der x1x3-Ebene
- an der x2x3-Ebene