Kopie von Gerade – Ebene
- Spaghetti (möglich ist auch ein Schaschlikspieß, Strohhalm oder zur Not auch ein dünner Stift)
- eine Spielkarte (möglich ist auch ein Notizzettel oder ein Stück Pappe)
- ggf. ein bisschen Knete/Klebeband

Aufgabe 1: Erarbeitung der möglichen Lagebeziehungen
a) Wie kann man deren gegenseitige Lage beschreiben? b) Verändere nun die Lage der Spaghetti und der Spielkarte. Welche verschiedenen Lagebeziehungen sind nun möglich?
Erarbeitung eines Fließdiagramms
Aufgabe 2: Übertragung in ein Koordinatensystem
Ziel ist es nun, die bisherigen Ideen in ein Koordinatensystem und schlussendlich ein Fließdiagramm zu überführen.
Folgende Begriffe/Konzepte solltest du dabei beherrschen:
Betrachte nun das Koordinatensystem mit der Geraden und der Ebene in Koordinatenform . Du findest die Geraden- und Ebenengleichung oben links in der Ecke. Du kannst die Gerade verändern, indem du die Koordinaten des Punktes mit Hilfe der Schieberegler anpasst. Du kannst auch die Parameter a, b, c, d der Koordinatenform der Ebene E (und damit auch den Normalenvektor ) mithilfe des Schiebereglers anpassen.
a) Ermittle eine Geraden- und eine Ebenengleichung, sodass die Geraden und die Ebene parallel zueinander sind.
b) Betrachte das Skalarprodukt des Normalenvektors der Ebene und des Richtungsvektors der Geraden. Was fällt auf und weshalb tritt dieses Phänomen auf? Fertige dafür eine kleine Skizze an.
Du kannst dafür auch dein Material vom Anfang des Arbeitsblattes nutzen und mithilfe von Knete oder Klebeband und einer Spaghetti einen Normalenvektor auf deine Ebene basteln.
c) Warum ist es sinnvoll, den Normalenvektor bzw. die Koordinatengleichung zu nutzen? Wäre auch die Nutzung eines Richtungsvektors der Ebene (in Parameterform) möglich?
d) Was müsste passieren, damit die Gerade in der Ebene liegt?
Tipp: Nutze zum Ändern der Perspektive die Items an der oberen rechten Ecke.
Aufgabe 3
Nutze nun dein Wissen aus der letzten Aufgabe und dein Wissen zu linearer Abhängigkeit. a) Fertige eine Skizze an (oder nutze dein Material vom Anfang des Arbeitsblattes), in der sich die Ebene und die Gerade orthogonal schneiden. Zeichne/Bastele dafür auch den Richtungsvektor der Geraden sowie den Normalenvektor der Ebene ein. > Lösung: https://t1p.de/j8uq0 b) Bilde nun ein Beispiel für eine Gerade und eine Ebene, die sich orthogonal schneiden, im GeoGebra Applett nach. Worauf musst du achten? Wie verhalten sich der Richtungsvektor und der Normalenvektor der Ebene? c) Ermittle nun ein Beispiel, in dem sich Gerade und Ebene schneiden. Was musst du ändern?
Aufgabe 4: Fließdiagramm
Fließdiagramm
Aufgabe 5: Schnittpunkt Gerade – Ebene
Bei Geraden und Ebenen ist es neben dem Fließdiagramm natürlich noch wichtig, den Schnittpunkt letztlich auch ermitteln zu können. a) Reaktiviere dafür dein Wissen zur Bestimmung des Schnittpunktes zweier Geraden. Beschreibe kurz deinen Vorgehen.
Beispielrechnung
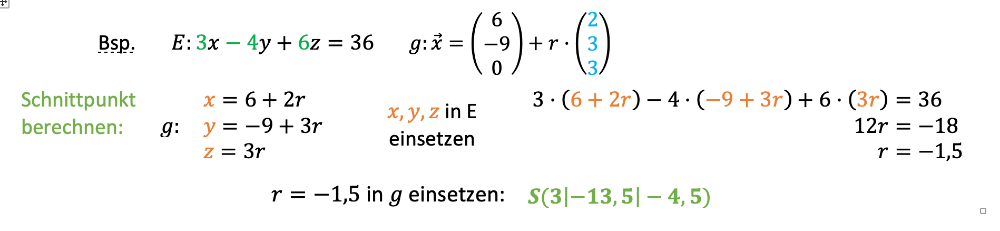
b) Errechne selbst den Schnittpunkt für die Gerade und der Ebene und erkläre dabei schrittweise dein Vorgehen.