Affine Abbildung Basiswechsel R2
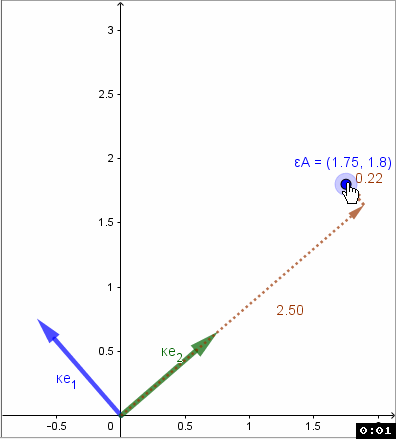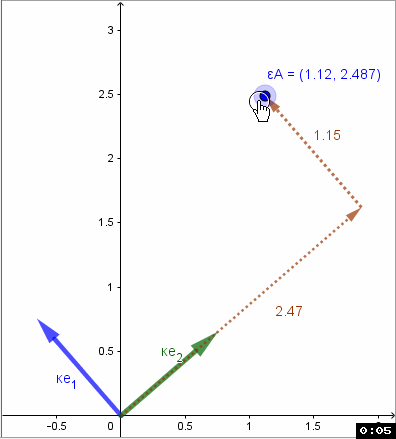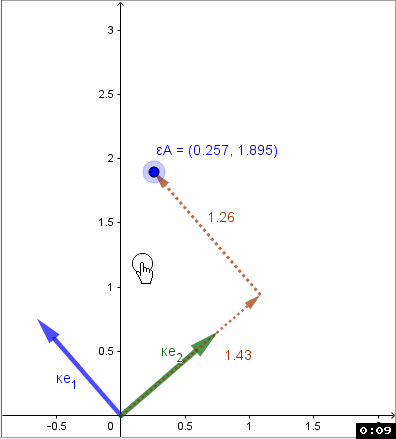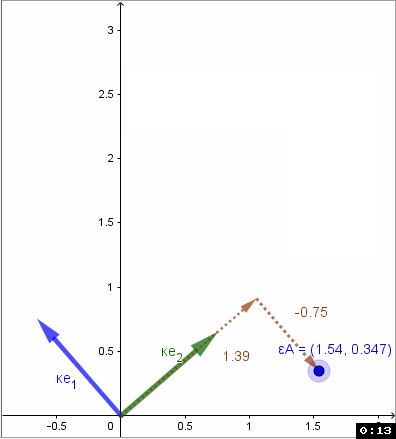
Die Basisvektoren K in einer Matrix {Ke1 , Ke2 } zusammengefast beschreiben eine Basistransformation von K nach E (Einheitsbasis): geschrieben ETK .
ETK= {Ke1 , Ke2 }
Die Umkehrung (also von E nach K) KTE = ETK-1 .
Die Abb α. oder genauer, EαE funktioniert auf der Einheitsbasis E. Um die Abbildung in K-Koordinaten zu haben müssen K Vektoren nach E konvertiert, die Bilder in EαE (EAE) berechnet und wieder in K dargestellt werden.
Also schreibt sich die Abb α: εAε εv + εb in der Basis K
EαE := EAE x + Eb
KαK := KTE EAE ETK + KTE Eb
KαK := ETK-1 EAE ETK + ETK-1 Eb
KαK := KAK x + Kb
App do not run in some versions of ggb6