Ruotare vuol dire ... cambiar base (con qualche vincolo)
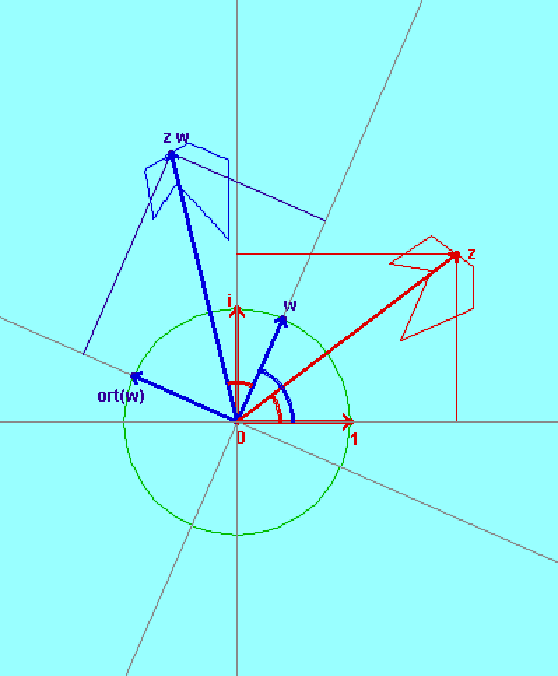
le rotazioni intorno all'origine
- La roto-omotetia Rw porta 1 in w. Nel caso accada che tale roto-omotetia porti il coniugato di w (ossia w⁻) in 1, diciamo che Rw è una rotazione (più correttamente: una rotazione intorno a 0) e che w è un numero complesso unitario.
- l'insieme dei numeri complessi unitari si chiama circonferenza unitaria (notazione: U): Sono elementi di U, ad esempio, 1, -1 , i, -i.
- ogni numero complesso z ≠ 0 si può esprimere in modo unico come prodotto z=r•u con r > 0 e con u unitario: r è detto modulo di z (notazione: |z|) e u è detto versore di z (notazione: vers(z))
- la versione geometrica di quanto appena detto consiste nel fatto che ogni roto-omotetia è esprimibile come trasformazione composta di rotazione e omotetia:
Rw = R|w|
 Rvers(w) = H|w|
Rvers(w) = H|w| Rvers(w) = Rvers(w)
Rvers(w) = Rvers(w) H|w|
H|w|
- importanti conseguenze e formule:
- numeri unitari: se w=a+b•i (con a e b reali), la condizione Rw(w) = 1 equivale a: w⁻•w = a2 + b2 = 1
- modulo: se z=x+y•i (con x e y reali), si ha: |z|2 = z⁻•z = x2 + y2. Si pone, per definizione: |0|=0
- versore: se z è un numero complesso non nullo, è |z|>0, e da z=|z|•vers(z) si ricava: vers(z)=(1/|z|)•z⁻
- chiusura moltiplicativa della circonferenza unitaria: se u e u' appartengono a U, allora u•u' è in U (infatti: u·u' · (u·u') = (u · u') · (u · u') = u · u · u' · u' = 1 · 1 = 1 )
- scomposizione del prodotto: z•w = (|z|•|w|) • [ vers(z)•vers(w) ]
- modulo e versore del prodotto: le uguaglianze z•w=|z•w|•vers(z•w) e z•w=(|z|•|w|)[vers(z)•vers(w)], alla luce dell'unicità dell'espressione di un numero complesso non nullo come prodotto di un numero positivo per uno unitario, comportano le uguaglianze: |z•w| = |z|•|w| e vers(z•w) = vers(z)•vers(w)
- numeri unitari e coniugazione: per un numero unitario u, la condizione u⁻•u =1 significa che u⁻ = 1/u
- rapporto di due numeri complessi: dati i numeri complessi w' e w≠0, l'equazione w'=z·w comporta, da una parte, che |w'|=|z|·|w|, e quindi |z| = |w'|/|w|, e da un'altra che vers(w')=vers(z)·vers(w), da cui segue vers(z)=vers(w')/vers(w). Pertanto il rapporto w'/w è definibile in modo unico ed è: z = w'/w = (|w'|/|w|)·vers(w')/vers(w)
- inversione algebrica e coniugazione: se z è non nullo, il reciproco di vers(z) è vers(z)⁻ e il reciproco di z = |z|•vers(z) è 1/z = (1/|z|) • vers(z)⁻.