Diseño del azulejo fundamental
Esta actividad pertenece al libro de GeoGebra La fábrica de teselados.
Como ya hemos adelantado, para que nuestra fábrica de teselados pueda comenzar a funcionar, necesita ser alimentada con un azulejo fundamental. Precisamente, en el diseño de este azulejo fundamental, junto al aporte de los dos vectores que van a dirigir sus traslaciones, reside el objetivo de cualquier proyecto didáctico en este contexto.
En las siguientes secciones se muestran varios ejemplos de azulejos ya diseñados, desde muy sencillos hasta bastante sofisticados. Sin embargo, veremos ahora algunas ideas básicas que pueden servir de ayuda.
Los triángulos equiláteros, los cuadrados y los hexágonos regulares son los únicos polígonos regulares que teselan el plano. Pero, como se verá en los ejemplos, podemos combinarlos de diversas formas. Además, los polígonos de partida no tienen por qué ser necesariamente regulares.
Ya hemos visto que un cuadrado tesela por traslación, pero son necesarios dos de ellos para teselar diferenciando colores. Así que, en este caso, nuestro azulejo fundamental ya no es cuadrado, sino rectangular.
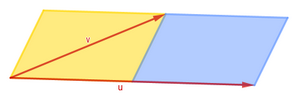
Del mismo modo, cualquier paralelogramo tesela por traslación, siendo sus vectores de traslación justamente los definidos por dos lados contiguos. Ahora bien, igual que antes, son necesarios dos de ellos para teselar diferenciando colores, como muestra la siguiente imagen. Observa que debemos ajustar los vectores de traslación para que no coincidan los colores al trasladar el azulejo, sino que vayan alternándose.
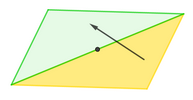
Si dividimos un paralelogramo cualquiera por la mitad, siguiendo una de sus diagonales, obtenemos un triángulo. Por lo tanto, a partir de cualquier triángulo podemos crear un azulejo fundamental sin más que reconstruir el paralelogramo correspondiente, reflejando el triángulo por el punto medio de uno de sus lados (lo que equivale a rotarlo 180° alrededor de ese punto), como muestra la siguiente imagen. (Existen más modos de teselar a partir de un triángulo, pero este es el más general y sencillo.)
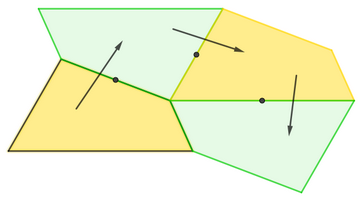
Cualquier cuadrilátero (incluso no convexo) también tesela el plano. Para crear el azulejo fundamental, podemos seguir un procedimiento similar al anterior, reflejando sucesivamente el cuadrilátero por el punto medio de uno de sus lados, como muestra la siguiente imagen. El octógono así conseguido ya es trasladable (se trata de una consecuencia del Teorema de Varignon).
¿Hay más posibilidades? Pues sí. Pero tampoco hace falta complicar demasiado el diseño. A partir de todas estas formas (polígonos regulares, triángulos y cuadriláteros), ya sea por composición de ellas o por el método de "quita y pon" (cortar un trozo del azulejo, rotarlo y volverlo a añadir adecuadamente, ver Hueso nazarí o Pajarita nazarí), las posibilidades son prácticamente infinitas. ¡Así que puedes dar rienda suelta a tu creatividad y crear tu propio teselado original!
Autor de la actividad: Rafael Losada.