Ränni

Pitkästä, 30 cm leveästä metalliliuskasta taitellaan ränni siten, että molemmilta pitkiltä sivuilta taitetaan 10 cm mittaiset palat ylös sopivaan kulmaan (katso kuva alla). Mikä on se kulma joka maksimoi muodostuvan rännin tilavuuden?
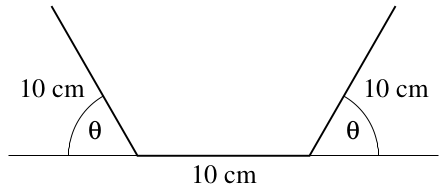
Oletetaan, että . Merkitään rännin korkeutta symbolilla . Rännin tilavuus maksimoituu silloin, kun sen poikkipinta-ala on suurimmillaan. Poikkipinta-ala on puolisuunnikas, jonka pinta-ala on
Avoimella välillä saavuttaa suurimman (ja pienimmän) arvonsa derivaatan nollakohdissa ja pisteissä, joissa derivaattaa ei ole määritelty. Koska on kaikkialla jatkuva ja derivoituva, ääriarvot löytyvät sen derivaatan nollakohdista.
Merkitään , jolloin saadaan
Tämän toisen asteen yhtälön ratkaisuna saadaan ja . Nyt siis jos
tai
Saaduista ratkaisuista määrittelyvälille kuuluu vain . Tutkimalla derivaatan merkkiä tämän nollakohdan ympärillä voidaan todeta, että se on maksimiarvo ja siten :n suurin arvo määrittelyvälillä. Eli siis kulman täytyy olla .