Merkwaardige lijnen in een driehoek construeren
Zwaartelijn van een driehoek construeren
VOORDAT JE BEGINT: als je iets hebt getekend dat je niet wil kan je dit ongedaan maken met de pijlen die je ziet rechts bovenaan in het tekenvenster.
Stap 1
- Teken in geogebra de punten A, B en C.
- Typ het GeoGebra-commando 'Veelhoek(A,B,C)' in de invoerbalk. Nu heb je driehoek ABC getekend. Deze driehoek heeft de naam 'driehoek 1' gekregen.
- Construeer nu de 3 zwaartelijnen. (Probeer dit eerst zelf vooraleer je "zwaartelijn construeren" verder leest.) Tip: Denk aan de definitie van een zwaartelijn.
- Teken het midden van de lijnstukken. Gebruik de knop 'Midden of middelpunt'.

- Teken de zwaartelijnen. Gebruik de knop 'Lijnstuk'.

- Teken nu het zwaartepunt.
- Kopieer de stijl van punt A naar je zwaartepunt. Gebruik de knop 'Stijl kopiëren'.

- Verschuif je hoekpunten.
- Probeer ook eens je zwaartepunt te verschuiven.
Zwaartelijn construeren
Proficiat!
Je tekende zonet het zwaartepunt van driehoek ABC.
Ken je nog de eigenschap van het zwaartepunt?
Indien niet, bekijk deze dan nog eens hieronder.
Indien wel, ga verder naar het construeren van een bissectrice.
Het zwaartepunt van een driehoek verdeelt elke zwaartelijn in twee stukken waarvan het stuk naar het hoekpunt dubbel zo lang is als het andere stuk.
Bissectrice (deellijn) van een driehoek construeren
Stap 1
- Teken in geogebra de punten A, B en C.
- Typ het GeoGebra-commando 'Veelhoek(A,B,C)' in de invoerbalk. Nu heb je driehoek ABC getekend. Deze driehoek heeft de naam 'driehoek 1' gekregen.
- Construeer nu de 3 bissectrices a.d.h.v. GeoGebra-commando's in de invoerbalk: Bissectrice(A,B,C) Bissectrice(B,C,A) Bissectrice(C,A,B)
- Teken het snijpunt van de bissectrices.
Bissectrice van een driehoek construeren
Proficiat!
Je tekende zonet de bissectrices van driehoek ABC.
Ken je nog de eigenschap van een bissectrice van een driehoek?
Indien niet, bekijk deze dan nog eens hieronder.
Indien wel, ga verder naar het construeren van een ingeschreven cirkel.
Een bissectrice van een hoek van een driehoek verdeelt de overstaande zijde in 2 stukken die zich verhouden als de aanliggende zijden.
Ingeschreven cirkel van een driehoek construeren
VOORDAT JE BEGINT: als je iets hebt getekend dat je niet wil kan je dit ongedaan maken met de pijlen die je ziet rechts bovenaan in het tekenvenster.
Stap 1
- Construeer de bissectrice van hoek A en van hoek B a.d.h.v. GeoGebra-commando's in de invoerbalk.
- Teken het snijpunt van de bissectrices. Dit punt krijgt de naam D. Het punt D is het middelpunt van de ingeschreven cirkel.
- Teken de loodlijn door punt D op het lijnstuk AB. Gebruik hiervoor de knop 'Loodlijn'.
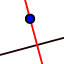
- Teken het snijpunt van de loodlijn en lijnstuk AB. Dit punt krijgt den naam E. Het lijnstuk DE is nu de straal van de ingeschreven cirkel.
- Teken de ingeschreven cirkel van driehoek ABC. Gebruik hiervoor de knop 'Cirkel met middelpunt door punt'.
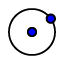
Proficiat!
Je tekende zonet de ingeschreven cirkel van driehoek ABC.
Weet je nog wat het middelpunt en de straal van de cirkel is?
Indien niet, lees de instructie nog eens opnieuw.
Indien wel, ga verder met het construeren van een hoogtelijn.
Hoogtelijn van een driehoek construeren.
Stap 1
- Teken in geogebra de punten A, B en C.
- Typ het GeoGebra-commando 'Veelhoek(A,B,C)' in de invoerbalk. Nu heb je driehoek ABC getekend. Deze driehoek heeft de naam 'driehoek 1' gekregen.
- Construeer nu de 3 hoogtelijnen. (Probeer dit eerst zelf vooraleer je "hoogtelijn construeren" verder leest.) Tip: Denk aan de definitie van een hoogtelijn.
- Teken het loodlijn uit een hoekpunt op de overstaande zijde. Gebruik de knop 'Loodlijn'.

- Teken nu het hoogtepunt.
- Verschuif de hoekpunten van driehoek ABC.
- Valt het hoogtepunt altijd binnen de driehoek?
Hoogtelijn van een driehoek construeren
Proficiat!
Je tekende zonet het hoogtepunt van driehoek ABC.
Ken je nog de eigenschap van de hoogte op de schuine zijde in een rechthoekige driehoek?
Indien niet, bekijk deze dan nog eens hieronder.
Indien wel, ga verder naar het construeren van een middelloodlijn.
De hoogte op de schuine zijde is een rechthoekige driehoek verdeelt de driehoek in twee driehoeken die gelijkvormig zijn met de gegeven rechthoekige driehoek.
Middelloodlijn van een driehoek construeren
Stap 1
- Teken in geogebra de punten A, B en C.
- Typ het GeoGebra-commando 'Veelhoek(A,B,C)' in de invoerbalk. Nu heb je driehoek ABC getekend. Deze driehoek heeft de naam 'driehoek 1' gekregen.
- Construeer nu de middelloodlijnen op alle drie de zijdes. (Probeer dit eerst zelf vooraleer je "middelloodlijn construeren" verder leest.) Tip: Denk aan de definitie van een middelloodlijn.
- Teken het midden van de lijnstukken. Gebruik hiervoor de knop 'Midden of middelpunt'.

- Teken de loodlijn door het middelpunt op het lijnstuk. Gebruik de knop 'Loodlijn'.

Proficiat!
Je tekende zonet de middelloodlijnen van driehoek ABC.
Je bent klaar met deze les.