4.2 El nombre del grupo cristalográfico
Como resumen de los apartados anteriores, podemos reseñar que hay cuatro isometrías, que son los movimientos en el plano que conservan las distancias. Dos de ellas mantienen la orientación: la traslación y la rotación. Las otras dos invierten la orientación: la simetría y la simetría con deslizamiento. En matemáticas se ha estudiado este tema desde la óptica de las estructuras y se ha demostrado a que hay exactamente 17 grupos llamados cristalográficos planos. Reciben ese nombre porque el estudio surge del trabajo de científicos y geómetras como Fedorov, que a finales del siglo XIX estudiaban la estructura de los cristales.
La estructura de grupo hace necesarias tres condiciones:
Lo primero que se hace es determinar un paralelogramo, llamado primitivo, que pueda generar el mosaico mediante dos vectores de traslación colocados sobre sus lados (no confundir con la baldosa mínima que puede ser aún más pequeña al poder utilizar isometrías distintas de la traslación). Con rectas paralelas a los lados del paralelogramo se organiza una trama. De todos los paralelogramos posibles, se toma aquel que tenga los vértices sobre centros de rotación de orden máximo. Si no hay centros de rotación (orden 1), hacemos coincidir los ejes de simetría con los lados o con las diagonales.
La notación establecida por la Unión Internacional de Cristalografía (Comité Español), también conocida como notación de Hermann-Mauguin, consta de cuatro símbolos ordenados: 
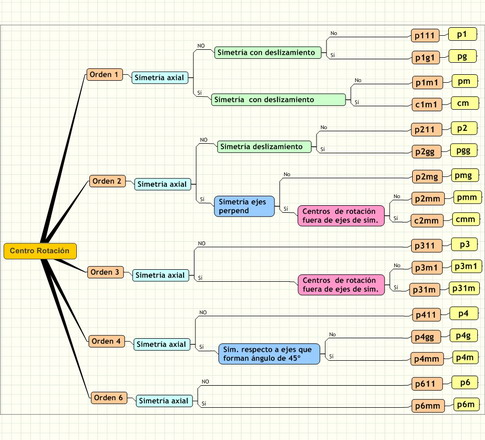En la página de Internet se ilustra cada grupo cristalográfico con uno o varios mosaicos. Los applets permiten la interacción sobre la construcción de varias maneras:
- Que exista un movimiento identidad (la traslación de vector nulo o el giro de 0º).
- Que cada movimiento tenga inverso, es decir, que cada isometría se pueda deshacer con otra (una traslación con otra de vector igual pero de sentido contrario, una simetría axial con otra que tenga el mismo eje, etc.).
- Que la composición de dos isometrías sea también una isometría del grupo (ley interna). Esto en los movimientos se traduce en ideas del tipo “dos simetrías de ejes paralelos es igual a una traslación de vector perpendicular a los ejes de módulo igual al doble de la distancia que separa los ejes”.
Lo primero que se hace es determinar un paralelogramo, llamado primitivo, que pueda generar el mosaico mediante dos vectores de traslación colocados sobre sus lados (no confundir con la baldosa mínima que puede ser aún más pequeña al poder utilizar isometrías distintas de la traslación). Con rectas paralelas a los lados del paralelogramo se organiza una trama. De todos los paralelogramos posibles, se toma aquel que tenga los vértices sobre centros de rotación de orden máximo. Si no hay centros de rotación (orden 1), hacemos coincidir los ejes de simetría con los lados o con las diagonales.
La notación establecida por la Unión Internacional de Cristalografía (Comité Español), también conocida como notación de Hermann-Mauguin, consta de cuatro símbolos ordenados: - Símbolo 1. Es c (“centrado”) cuando el paralelogramo primitivo es un rombo que se puede enmarcar centrándolo en un rectángulo y p (“primitivo”) en cualquier otro caso. De los 17 grupos, sólo dos son centrados: cm y cmm.
- Símbolo 2. El mayor orden de rotación que podamos encontrar. Puede ser 1 (ángulo de 360º), 2 (ángulo de 180º), 3 (ángulo de 120º), 4 (ángulo de 90º) ó 6 (ángulo de 60º). Cuando un mosaico tiene un centro de rotación de un orden determinado, también tendrá otros centros de órdenes divisores.
- Símbolo 3. Corresponde al tipo de simetría y puede tener dos símbolos: m (“mirror” = espejo) simetría especular o axial y g (“glide” = deslizamiento), cuando tiene simetría con deslizamiento.
- Símbolo 4. La misma clasificación anterior, respecto a la presencia o no de un segundo tipo de ejes de simetría (m o g).
En la página de Internet se ilustra cada grupo cristalográfico con uno o varios mosaicos. Los applets permiten la interacción sobre la construcción de varias maneras:
- Los elementos de simetría del mosaico aparecen y desaparecen al accionar los interruptores de la parte inferior.
- Se puede reproducir una secuencia animada de la construcción de la baldosa generadora del mosaico a partir de un polígono básico que transforma su silueta para adquirir una nueva forma o se descompone en piezas más pequeñas que se unirán a otras iguales a ella.
- La composición del mosaico a partir de la nueva forma generada utilizando las isometrías.