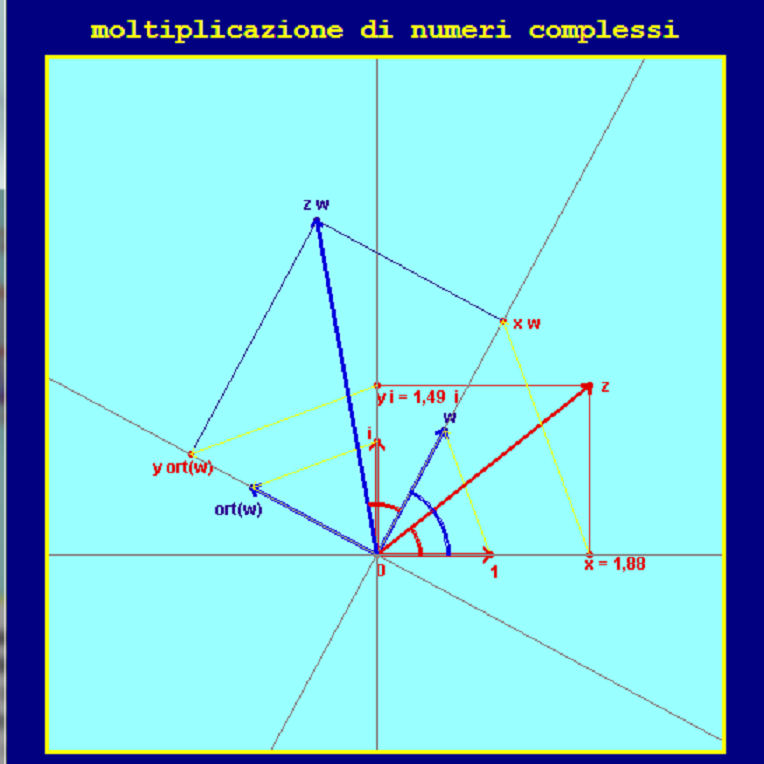
moltiplicazione punto per punto - versione 1
Moltiplicazione A∙B con A e B entrambi punti del piano cartesiano.
A∙B è il punto realizzato nel sistema di riferimento ( 0 , B , B⊥ )
con le coordinate che A ha nel sistema di riferimento ( 0 , 1 , i ),
ossia con A_x e A_y .
Vedi ▶ http://tinyurl.com/moltiplicazione
moltiplicazione in C
- estensione della moltiplicazione a coefficienti reali alla moltiplicazione a coefficienti complessi: se z=x+yi, definiamo: z*w := x•w + y•ort(w). Dal momento che se z=x si ha y=0 e di conseguenza x*w = x•w. l'operazione * estende a CxC la moltiplicazione • già definita su RxC. Pertanto continueremo a denotare col simbolo • (oppure, come già abbiamo spesso fatto, senza alcun simbolo) la nuova operazione * , che continueremo a chiamare ancora moltiplicazione, precisamente moltiplicazione in C oppure moltiplicazione a coefficienti complessi. Riassumendo:
- moltiplicazione a coefficienti reali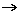: ( x , w )
x•w
- moltiplicazione a coefficienti complessi: ( x + y•i , w ) 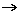x•w + y•ort(w)
- cambiamento di base: la corrispondenza z 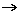z•w associa al numero z, di coordinate x e y realizzate nel sistema di riferimento (detto anche "base") costituito da 1 e i, in quanto x+yi=x•1+y•i=x•1+y•ort(1), quel punto che ha le stesse coordinate x e y realizzate nel sistema di riferimento costituito da w e ort(w), ossia x•w+y•ort(w), pertanto realizza le coordinate x e y rispetto a w, ovvero in una nuova scala in cui 1 viene sostituito da w. Per questo fatto tale corrispondenza viene chiamata omotetia (termine greco che significa uguale disposizione; confronta le parole "omotetico" e "antitetico") in C. Riassumendo, possiamo dire che z•w rappresenta z realizzato nella scala (o base) di w invece che nella scala (o base) di 1
- proprietà:
- moltiplicazione per i: abbiamo: i w = ( 0 + 1i ) w = 0w + 1 ort(w) = ort(w) e z i = ( x + yi ) i = xi + y ort(i) = xi + y(-1) = -y + xi = ort(z). In particolare: i2 = i•i = -1. Pertanto: moltiplicare un numero complesso per l'unità immaginaria i significa ortonormalizzarlo
- espressione algebrica del prodotto: (x + yi)•(x' + y'i) = x•(x'+y'i) + y•ort(x'+y'i) = x•(x'+y'i) + y•(-y'+x'i) = ( x x' - y y' ) + ( x y' + x' y )i
- commutativa: z•w = w•z (prova a dimostrare da solo la commutatività)
- associativa: (z•w)•v = z•(w•v) (prova a dimostrare da solo l'associatività)
- distributiva: (z+w)•v = (z•v) + (w•v) (la commutatività permette di enunciare una sola distributività, senza distinguere quella sinistra da quella destra) (prova a dimostrare da solo la distributività)
- neutralità dell'uno: 1•z = z (questa proprietà è del tutto immediata, in quanto 1 è reale)
- coniugato del prodotto: z • w = z • w (prova a dimostrare da solo questa proprietà). Fra i sette operatori isometrici coordinati distinti dall'identità, conj è l'unico che conserva il prodotto; tutti invece, come già visto, conservano le combinazioni lineari.
Come costruire il prodotto di numeri complessi tramite rette parallele
