Sistema de ecuaciones NO lineales
Una ecuación es no lineal cuando la o las incógnitas de la ecuación se multiplican (o dividen) entre sí o cuando tienen exponentes.
Ejemplos:
- Una ecuación de segundo grado (como ) es una ecuación no lineal.
- La ecuación no es lineal porque hay dos incógnitas que se multiplican.
- La ecuación no es lineal porque una de las incógnitas está en el exponente de una potencia.
Problema 27
El producto de las edades de dos hermanos es 162 y su cociente es 2. ¿Cuántos años tienen?
Solución:
Si las edades son x e y, su producto es
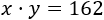
Y su cociente es
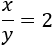
El sistema de ecuaciones no lineales del problema es
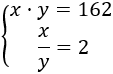
Despejamos la x de la segunda ecuación:
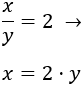
Y sustituimos en la primera ecuación:
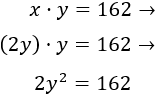
Resolvemos la ecuación de segundo grado:
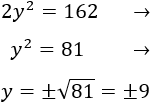
Como y representa una edad, debe ser no negativo. Por tanto, y=9.
Calculamos x a partir de y=9:
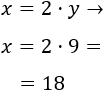
La solución del sistema es
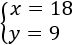
Sus edades son 9 y 18 años.
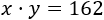
Y su cociente es
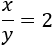
El sistema de ecuaciones no lineales del problema es
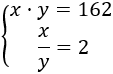
Despejamos la x de la segunda ecuación:
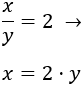
Y sustituimos en la primera ecuación:
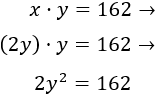
Resolvemos la ecuación de segundo grado:
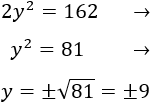
Como y representa una edad, debe ser no negativo. Por tanto, y=9.
Calculamos x a partir de y=9:
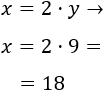
La solución del sistema es
Sus edades son 9 y 18 años.Otros problemas
Problema 28: La edad de Ana María es el cuadrado de la edad de su hija. Además, dentro de 9 años, su edad será el triple que la de su hija. ¿Qué edad tiene Ana María?
Problema 29: Sandro y Ezequiel son hermanos y el producto de sus edades es igual a la edad de su padre. Sandro es 8 años menor que Ezequiel y la suma de su edad y la de su padre es igual a 36. ¿Qué edad tiene Ezequiel?
Problema 30: Aurelio, Carlos y José son hermanos. José es el mayor de los tres y su edad es igual a la suma de los cuadrados de las edades de sus hermanos. Dentro de un año, la edad de Carlos será el doble que la de Aurelio y dentro de 22 años, la edad del mayor será igual a la suma de las edades de sus hermanos. ¿Qué edad tiene José?
Problema 31: La suma de la edad de Gerardo y la de su sobrino es 38. Dentro de 5 años, la edad del Gerardo será la octava parte del cuadrado de la edad de su sobrino. ¿Qué edad tiene Gerardo?
Problema 32: El producto de las edades actuales de dos amigos es 42 y dentro de 5 años será 132. ¿Qué edades tienen?
Enlace a las soluciones de los problemas: Problemas de edades (ecuaciones y sistemas)
Temas relacionados: