Finding a self-intersection points of a Rose -Curve (Polyline approximation). 1
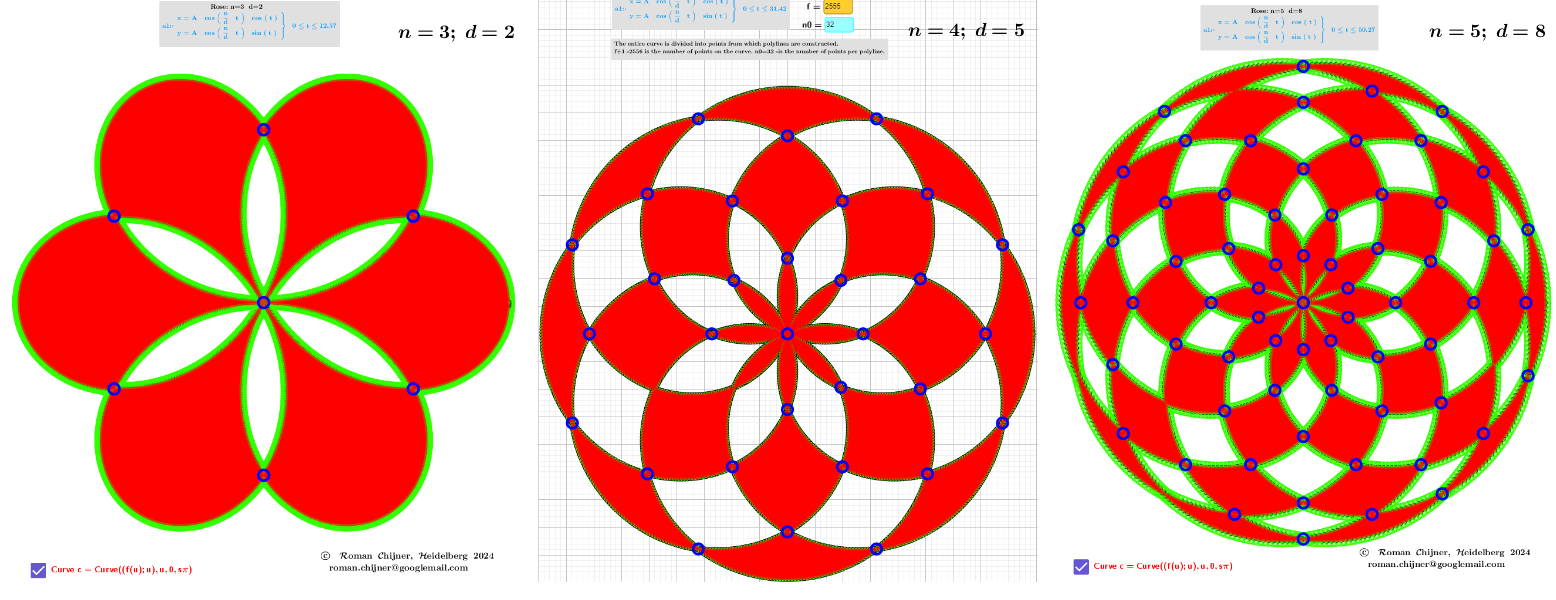
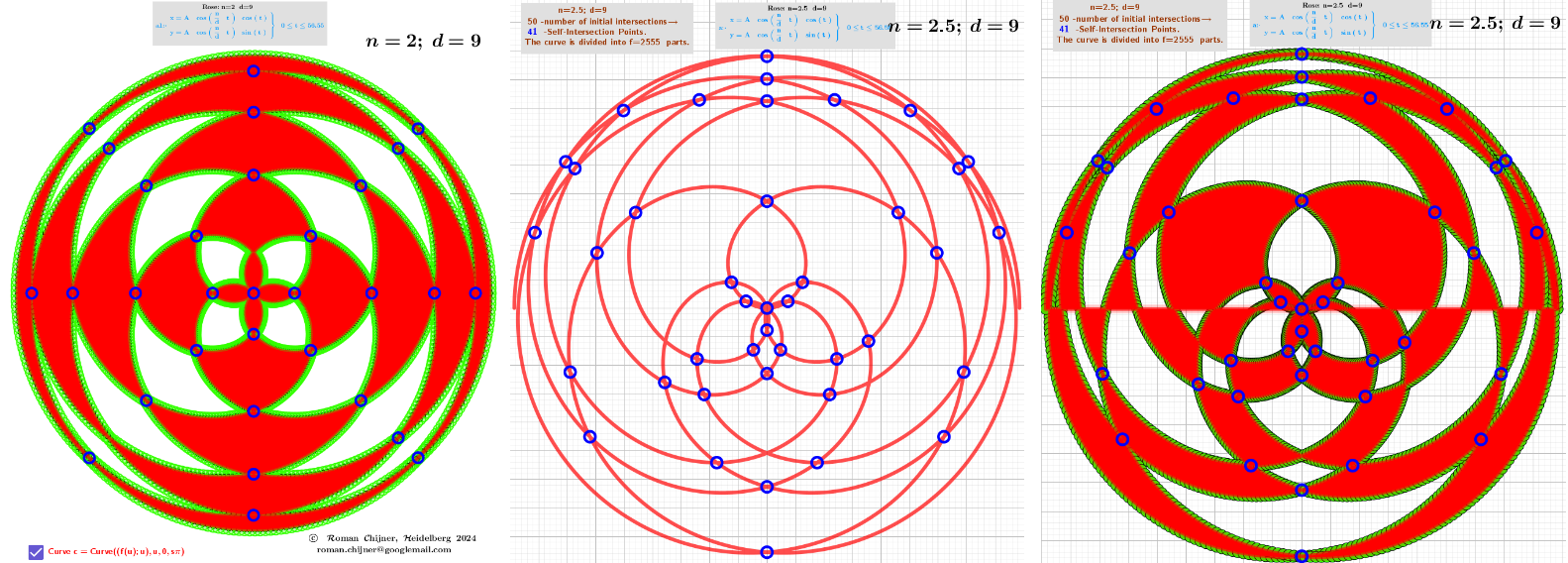
In this applet, the rose curves are considered.
The self-intersection points of the curve are approximated as intersection points of separate polylines whose points are partition points of the original curve. Each polyline has the same number of points. The following problems occur.
1. Sometimes the intersection of the polylines is not at the self-intersection of the curve, and you have to search for it separately or change the number of points in the polylines.
2. When selecting a curve parameter, it should not "go over itself". This leads to "many" self-intersections.
3. Numerical calculations lead to the appearance of many nearby intersections. Their filtering was done by the applet method.
The intersection objects are not defined in the algebra, but in the applet script. The applet loads faster and all changes are easily implemented.
Unlike the work of an applet downloaded to a desktop computer, here you have to wait a few minutes for the script to work.
Finding the points of self-intersection for the Rose curve at n = 4 and d = 7
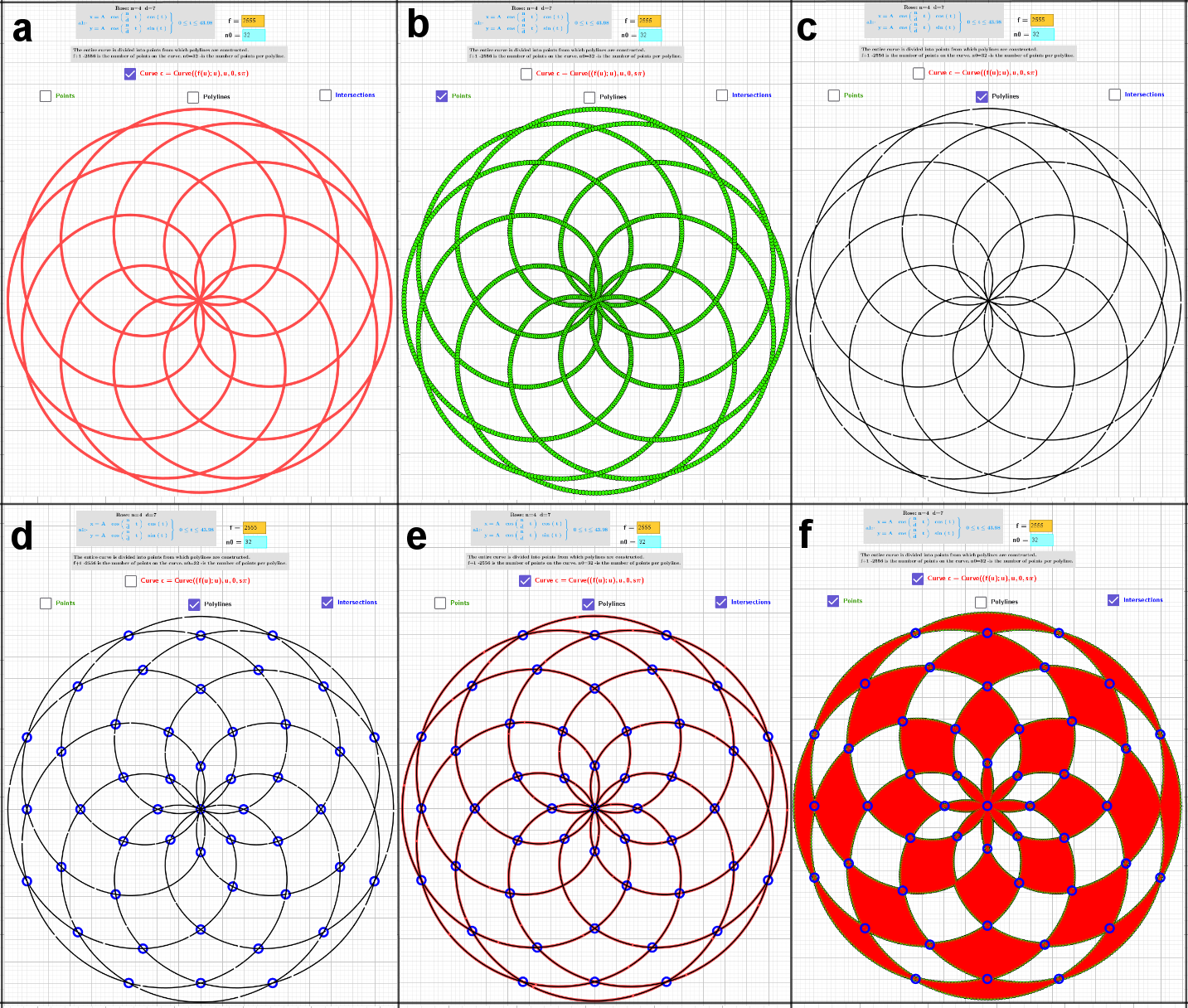
Table of images of the rose curve for some parameters: