Árbol pitagórico
Árbol Pitagórico
El árbol de Pitágoras es un fractal plano propuesto en 1942 por el profesor de matemáticas Albert E. Bosman. El nombre del fractal se debe a que cada trío de cuadrados en contacto es la típica figura que se utiliza para demostrar geométricamente el teorema de Pitágoras.
Construcción:
El árbol de Pitágoras es el límite de una construcción iterativa que comienza con un cuadrado al que se le van añadiendo cuadrados cada vez más pequeños:
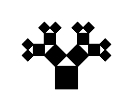
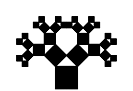
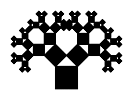
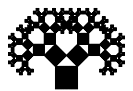
Por cada cuadrado añadido en una iteración, se añaden otros dos cuadrados en la siguiente, entonces...
- El paso inicial es un cuadrado de lado (por comodidad, suponemos )
- En la primera iteración, se añaden dos cuadrados de lado en las esquinas superiores del cuadrado como se muestra en la siguiente figura (formado ángulos de 45°):
- En las siguientes iteraciones, se repite el paso anterior en cada unos de los nuevos cuadrados añadidos en el paso anterior:
- Secuencia con las primeras iteraciones:
Por cada cuadrado añadido en una iteración, se añaden otros dos cuadrados en la siguiente, entonces...
a) ¿Cuál es el número de cuadrados nuevos en la iteración ?
b) ¿Cuál es el número total de cuadrado en la iteración ?
En el árbol de Pitágoras, el ángulo α que forman los lados de los cuadrados que se añaden en cada iteración es de 45°. Si cambiamos el ángulo y, por tanto, el tamaño de los cuadrados, obtenemos otros árboles.
Por ejemplo, si el ángulo que forma el cuadrado de la izquierda es y el de la derecha es , tenemos el siguiente árbol:
Considera la sucesión de figuras presentadas al comienzo, en la que se parte de un cuadrado de lado de longitud 1. Sobre uno de sus lados se construyen dos cuadrados iguales cuyos lados forman un ángulo recto, es decir, que la región que delimitan los cuadrados es un triángulo isósceles y rectángulo.
Sea la sucesión del área total de los cuadrados construidos en el paso (no se tiene en cuenta si los cuadrados se superponen).
c) Halla la razón de semejanza que existe entre el cuadrado construido en el paso inicial y los dos cuadrados más pequeños que se agregan en el paso siguiente. Indica qué semejanzas se deben aplicar para transformar el cuadrado inicial en cada uno de los dos que se agregan en el paso siguiente.
d) Halla los primeros tres términos de y calcula el área de los infinitos cuadrados que forman el árbol pitagórico (halla )
e) Calcula
f) Justifica por qué no está acotada.