Google Classroom
GeoGebraGeoGebra Classroom
GeoGebra

Completing the square and vertex form (AASL 2.6)

Author:Cliff Packman, David T, Kawa Chan

Keywords

EnglishJapaneseKoreanChinese Simplified
Completing the Square平方完成완전제곱식配方法
Vertex Form頂点形式정점 형식顶点式
Quadratic Equation二次方程式이차방정식二次方程
Axis of Symmetry対称軸대칭축对称轴
General Form to Vertex Form Conversion一般形から頂点形への変換일반형에서 정점형으로의 변환一般形式转顶点形式
Parabola放物線포물선抛物线
Coefficient係数계수系数
Graph of Quadratic Function二次関数のグラフ이차함수의 그래프二次函数图像
Standard Form標準形표준형标准形式
Line of Symmetry対称線대칭선对称线
Image

Inquiry questions

Factual Inquiry Questions
  • What is the process of completing the square for a quadratic equation?
  • How can completing the square be used to convert a quadratic equation into vertex form?
Conceptual Inquiry Questions
  • Why is completing the square a valuable method for solving quadratic equations, especially compared to factoring or using the quadratic formula?
  • How does completing the square provide insight into the graph of a quadratic function, particularly its vertex and axis of symmetry?
Debatable Inquiry Questions
  • Is completing the square more intuitive and beneficial for understanding the properties of quadratic functions than other methods of solving quadratics?
  • Can the technique of completing the square be considered foundational for more advanced topics in algebra and calculus? How so?
  • How might the teaching of completing the square evolve with the integration of technology in mathematics education, especially with tools that can automatically solve and graph quadratic equations?
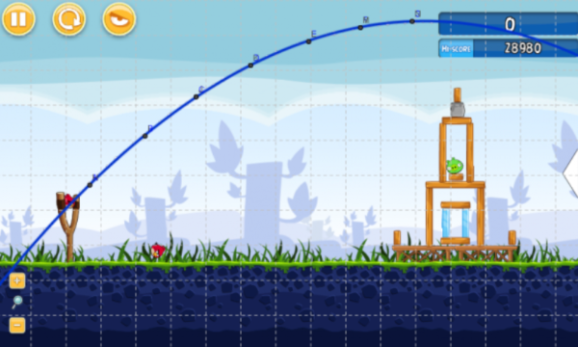
Image
Part 1- Exploring the vertex form, The Vertex Voyage Welcome aboard the Vertex Voyage, where we chart the path of parabolas and uncover the mysteries of their vertices! Let's navigate through the world of quadratic functions with these engaging challenges.

What is the effect on the parabola of changing the h and k values?

Check my answer

Expansion Expedition: Take the vertex form and expand it to get the general form . Do this for a parabola with a vertex at (3, -7) and a = 2.

Check my answer

Coefficient Cruise: Set sail on the coefficient sea by altering '' in the vertex form. What happens to the parabola when '' is greater than 1? Less than 1? Negative? Sketch your findings in your book.

Check my answer

Part 2 - Completing the square

We've seen that vertex form is useful for finding the vertex but what do we do if we have the equation in general form. This part explores moving from general form to

Standard Form Shift: Notice the equation . It's in general form! Can you rewrite it in vertex form by completing the square? Check your answer with applet below. Explain the general process from converting from general form to vertex form.

Check my answer

Standard Form Shift: Notice the equation . It's in standard form! Can you rewrite it in vertex form by completing the square? Show your work and check it by comparing the vertex.

Check my answer

Treasure of the Axis: The line of symmetry is the treasure map's "X marks the spot." If our vertex is at , where do you predict the line of symmetry is? Verify your prediction algebraically.

Check my answer

Expansion Expedition: Take the vertex form and expand it to get the standard form. Do this for a parabola with a vertex atand . Check your work by comparing the expanded form to the standard form.

Check my answer
Chart your findings and share them with your fellow math explorers. Keep a log of your discoveries, and remember, in the world of quadratics, every solution brings a new perspective. Happy voyaging!

Part 2 - Checking your understanding

Completing the square can be useful for putting the equation into vertex form. It can also be used for solving quadratic equations. Check out this video.

Question 1: Complete the square for the quadratic equation .

Select all that apply
  • A
  • B
  • C
  • D
Check my answer (3)

Question 2: What is the vertex of the quadratic equation ?

Select all that apply
  • A
  • B
  • C
  • D
Check my answer (3)

Question 3: Complete the square for the quadratic equation x^2 - 4x + 4.

Select all that apply
  • A
  • B
  • C
  • D

Question 4: What is the vertex of the quadratic equation ?

Select all that apply
  • A
  • B
  • C
  • D
Check my answer (3)

Question 5: Complete the square for the quadratic equation .

Select all that apply
  • A
  • B
  • C
  • D
Check my answer (3)

Question 6: What is the vertex of the quadratic equation ?

Select all that apply
  • A
  • B
  • C
  • D
Check my answer (3)

Question 7: Complete the square for the quadratic equation 3x^2 - 6x + 9.A) 3(x - 1)^2 + 6B) 3(x + 1)^2 - 6C) 3(x - 1)^2D) 3(x - 1)^2 + 9Correct Answer: A) 3(x - 1)^2 + 6

Question 8: What is the vertex of the quadratic equation ?

Select all that apply
  • A
  • B
  • C
  • D
Check my answer (3)
We are now ready to tackle some exam-style questions. Try Question 4, 5 ,17, 19, 20, 24, 25, 28 from the quadratic pack. These all involve completing the square (vertex form).

[MAA 2.2] QUADRATICS

[MAA 2.2] QUADRATICS.pdf

[MAA 2.2] QUADRATICS.pdf

[MAA 2.2] QUADRATICS_solutions

[MAA 2.2] QUADRATICS_solutions.pdf

[MAA 2.2] QUADRATICS_solutions.pdf

Lesson Plan- Completing the Square and Understanding Vertex Form

Lesson Plan- Completing the Square and Understanding Vertex Form.pdf

Lesson Plan- Completing the Square and Understanding Vertex Form.pdf

Completing the square and vertex form- Intuition pump (thought experiments and analogies)

Completing the square and vertex form.pdf

Completing the square and vertex form.pdf

New Resources

Discover Resources

Discover Topics