Weg-Zeit - Abfangkurs - Torpedo-Rechner
Position Start P:=(xP,yP)
Position Ziel T:=(xT,yT)
Kurs des Ziels(mit normiertem Vektor k_T) kurs_T(t):=T + t*v_T*(xk,yk)
Geschwindigkeiten Ziel v_T, Abfang v_S
v=s/t ===> gleiche Zeit t zum Treffpunkt
===> t=s/v
(kurs_T(t) - T)² (kurs_T(t) - P)²
------------ = --------------
v_T² v_S²
===>
t = (v_T*(k_T*(T-P))+sqrt(k_T^2*(T-P)^2*(v_S^2 - v_T^2) + (k_T*(T-P))^2*v_T^2))/(k_T^2*( v_S^2 - v_T^2))
t=(-xk v_T xP + xk v_T xT - yk v_T yP + yk v_T yT +
sqrt(xk² v_S² xP² - 2xk² v_S² xP xT + xk² v_S² xT² + xk² v_S² yP² - 2xk² v_S² yP yT + xk² v_S² yT² - xk² v_T² yP² + 2xk² v_T² yP yT - xk² v_T² yT² + 2xk yk v_T² xP yP - 2xk yk v_T² xP yT - 2xk yk v_T² xT yP + 2xk yk v_T² xT yT + yk² v_S² xP² - 2yk² v_S² xP xT + yk² v_S² xT² + yk² v_S² yP² - 2yk² v_S² yP yT + yk² v_S² yT² - yk² v_T² xP² + 2yk² v_T² xP xT - yk² v_T² xT²))
/ (xk² v_S² - xk² v_T² + yk² v_S² - yk² v_T²)

Applet
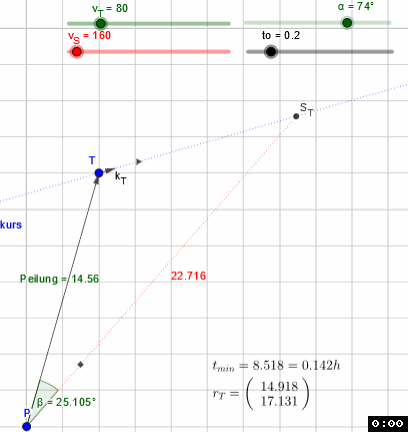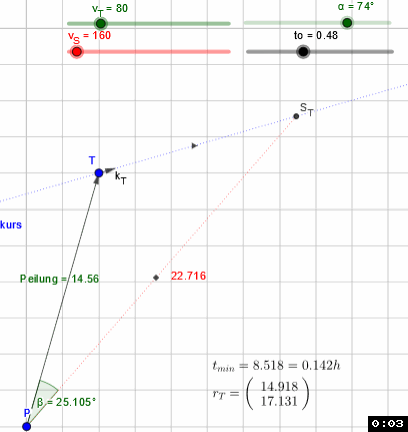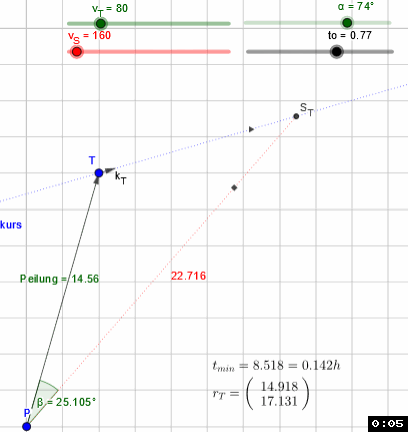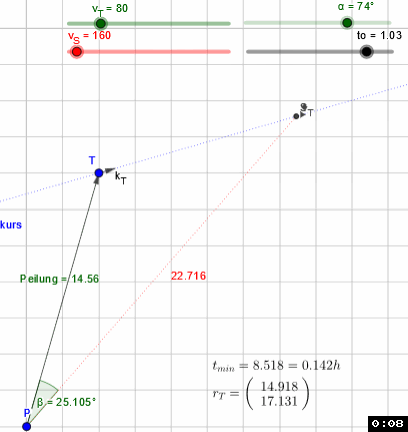
P(0,0) peilt T(4,14) in 14.56 km Entfernung mit 100 km/h auf Kurs 70° (Kursvektor kT(sin(a),cos(a)), yAchse Na=0) an. Der Treffpunkt ST befindet sich in 26.419 km Entfernung im Winkel von 27.556° zum Peilvektor. Bei einer Eigengeschwindigkeit von 175 km/h auf dem Kursvektor rT erreicht P T nach 9.058 min (0.151h).
Begegnung (Rendezvous)
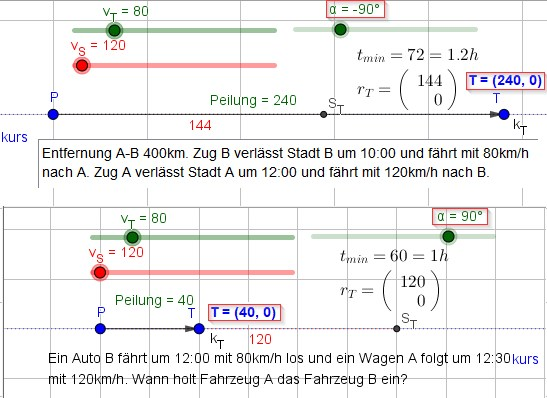
a=-90° ===> T fährt auf P(0,0) zu ===> nach to=2 h sind 160 km zurückgelegt und T befindet sich um 12:00 an Strecken-Punkt 400-160 ===> T=(240,0) ===> Begegnung nach to+1.2h (72min) bei Strecken-Punkt ST=(144,0).
Einholvorgang
a=90° ===> P(0,0) folgt T ===> T ist 30 min mit 80km/h unterwegs, befindet sich nach to=0.5h am Strecken-Punkt (40,0) ===> nach to+1h (60 min) holt P T ein - beide haben 120 km zurückgelegt.