Trigonometric Ratios
- Author:
- Michael Horvath
- Topic:
- Trigonometry
(Move the point labeled "Move" to adjust the dimensions of the triangle.)
(Move the point labeled "Move" to adjust the dimensions of the triangle.)
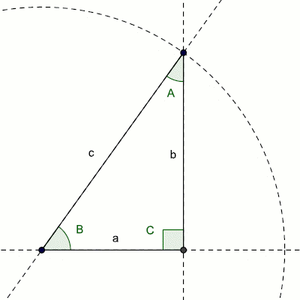
Sides of the right triangle:
Adjacent = a
Opposite = b
Hypoteneuse = c
Angles of the right triangle:
the angle opposite a = A
the angle opposite b = B
the angle opposite c = C
SOHCAHTOA:
SOH: Opposite / Hypoteneuse = sin(θ) = b / c
CAH: Adjacent / Hypoteneuse = cos(θ) = a / c
TOA: Opposite / Adjacent = tan(θ) = b / a
Hypoteneuse / Opposite = csc(θ) = c / b = 1 / sin(θ)
Hypoteneuse / Adjacent = sec(θ) = c / a = 1 / cos(θ)
Adjacent / Opposite = cot(θ) = a / b = 1 / tan(θ)
Other Functions:
1 = csc(θ)^2 - cot(θ)^2
1 = sec(θ)^2 - tan(θ)^2
1 = sin(θ)^2 + cos(θ)^2
1 = sec(θ) - exsec(θ)
1 = csc(θ) - coexsec(θ)
1 = vers(θ) + cos(θ)
1 = sin(θ) + covers(θ)
hav(θ) = vers(θ) / 2
Pythagorean Theorem:
c^2 = a^2 + b^2
Law of Sines:
2 * r = a / sin(A) = b / sin(B) = c / sin(C)
where "r" is the radius of the circumcircle
Law of Cosines:
cos(A) = (c^2 + b^2 - a^2) / (2 * b * c)
Law of Tangents:
(a + b) / (a - b) = tan((A + B) / 2) / tan((A - B) / 2)
Dot Product:
A · B = cos(θ) = xA * xB + yA * yB
where A and B are vectors with lengths equal to 1