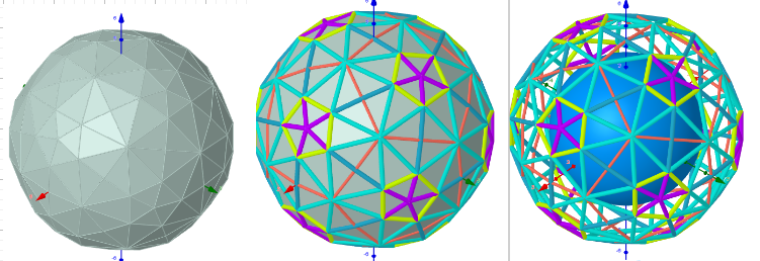
Images . Rhombicosidodecahedron from Biscribed Pentakis Dodecahedron for the case of trisection of its 1st-order segments

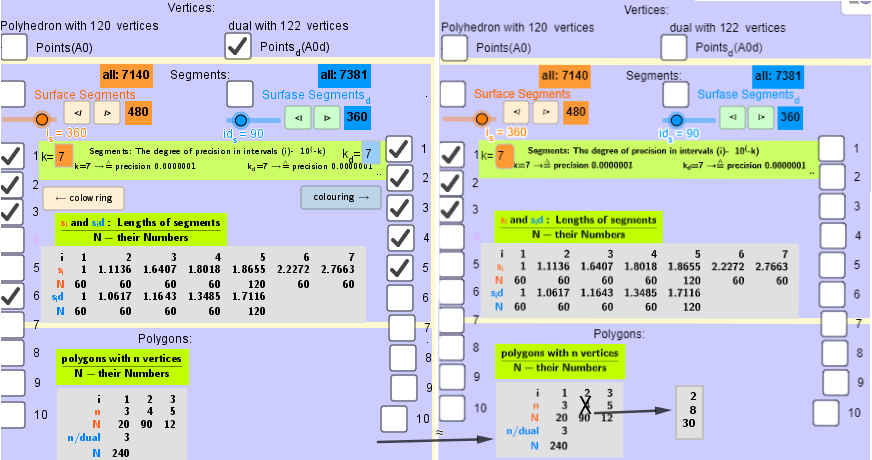
Elements in polyhedron Biscribed Pentakis Dodecahedron(1)
Vertices: V = 120.
Faces: F =122. 20{3}+(30+60){4}+12{5}
Edges: E =240. 60+60+60+60- The order of the number of edges in this polyhedron are according to their length.
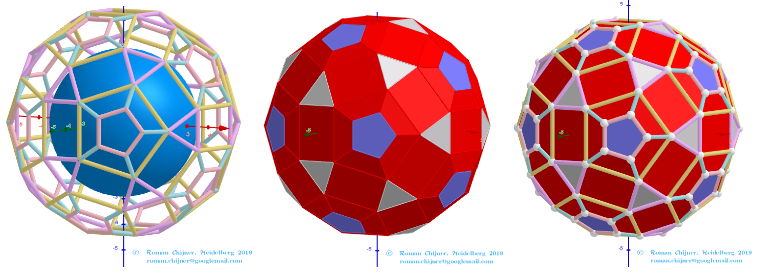
![[size=85] If we assume that all quadrilaterals lie in the same plane, then our polyhedron approximately looks like
ht[url=https://robertlovespi.net/2014/06/02/zonish-versions-of-the-rhombicosidodecahedron/]tps://robertlovespi.net/2014/06/02/zonish-versions-of-the-rhombicosidodecahedron/[/url]
Elements in polyhedron Biscribed Pentakis Dodecahedron(1)
[b]Vertices:[/b] V =120.
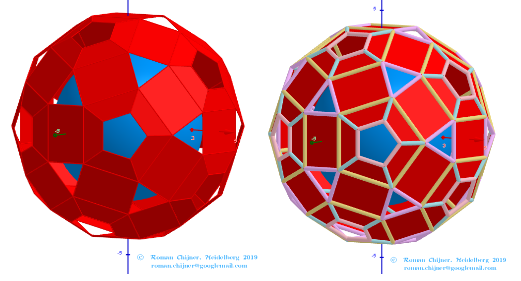
[b]Faces [/b]F =62. 20{3}+(30){8}+12{5}
[b]Edges:[/b] E =180. 60+60+60- The order of the number of edges in this polyhedron according to their length.[/size]](https://www.geogebra.org/resource/trnu6un9/ZK0xqw3pVztE5D1R/material-trnu6un9.png)
The elements of the dual to the Biscribed Pentakis Dodecahedron(1):
Vertices: V = 122.
Faces: F =240. 240{3}
Edges: E =360. 60+60+60+60+120- The order of the number of edges in this polyhedron are according to their length.