1-1 Désintégration radioactive : modélisation et simulation
Simulation avec GeoGebra puis Python
On présente ici deux simulations, une avec GeoGebra puis une avec Python d'une même modélisation mathématique de la désintégration radioactive.
Vous trouverez ici un fichier tableur Excel reproduisant la même simulation.
Modélisation :
On imagine avoir 100 noyaux radioactifs.
On suppose qu'à chaque étape (représentant un intervalle de temps), chaque noyau se désintégrera avec probabilité p, et ce indépendamment des autres noyaux.
La probabilité p est fixée par le curseur rouge. En faisant varier p, cela relance les nombres aléatoires du tableau.
Explications sur le contenu du tableur.
Les lignes du tableur de 5 à 104 correspondent aux états des 100 noyaux :
- 1 si le noyau est présent
- 0 s'il est désintégré
=Si(B5 ≟ 1 ∧ AléaEntreBornes(0, 100) < 100 (1 - $B$1), 1, 0)
qui signifie : Si en B5 il y a un 1 et qu'un tirage aléatoire entre 0 et 100 donne un nombre inférieur à 100(1-p), alors le noyau reste présent (1), sinon il n'y a plus de noyau (0).Avec Python
La fonction Python ci-dessous permet de simuler la même chose.
from random import*
def compte_noyaux_restants(n,p):
N=n
for i in range(n):
if random() < p:
N=N-1
return N
Par exemple compte_noyaux_restants(10000,0.02) renvoie le nombre de noyaux restants après une étape si on a initialement 10000 noyaux et qu'ils se désintègrent avec probabilité 0.02
On peut ensuite créer une liste du nombre de noyaux restants jusqu'à ce qu'il ne reste plus que 1% des noyaux.
def Liste_nb_noyaux_restants(n,p):
L=[]
N=n
while n>0.01*N:
L.append(n)
n=compte_noyaux_restants(n,p)
return L
On peut alors tracer le graphique avec le module matplotlib :
import matplotlib.pyplot as plt
n=40000
L=Liste_nb_noyaux_restants(n,1/6)
m=len(L)
plt.plot(range(m),L, linestyle = 'none', marker = '.')
plt.show()
Capture d'écran d'un programme Python pour p=1/6 et 40000 noyaux initiaux
Ci dessous se trouve une interface en ligne pour Python, via le site repl.it.
La fenêtre du haut contient le code Python que vous pouvez modifier.
La fenêtre noire en dessous est la console. Utilisez-la pour exécuter une des fonctions. Par exemple :
compte_noyaux_restants(10000, 0.02)
vous renverra le nombre de noyaux restants après une simulation avec n=10000 noyaux se désintégrant chacun avec probabilité p=0,02.
Le code produit aussi un graphique qui est visible en cliquant en haut à gauche sur l'icone document (Files) puis en choisissant graphique.png.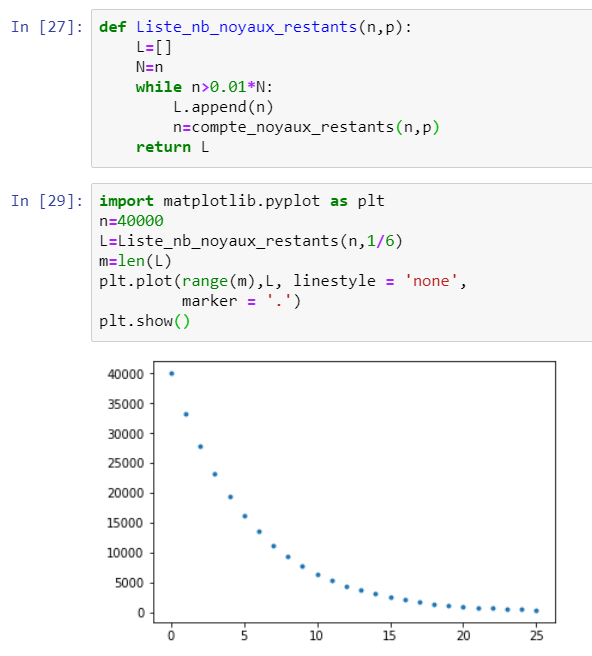
<iframe height="400px" width="100%" src="https://repl.it/@IAIPRacver/Desintegration-radioactive?lite=true" scrolling="no" frameborder="no" allowtransparency="true" allowfullscreen="true" sandbox="allow-forms allow-pointer-lock allow-popups allow-same-origin allow-scripts allow-modals"></iframe>