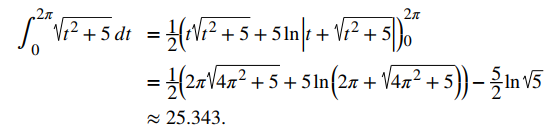Longitud de arco
Antes que nada, recordamos que una circunferencia es el contorno (perímetro) de un círculo. El perímetro de un círculo es una circunferencia.Un arco de circunferencia es una porción de una circunferencia.Ejemplo: Dos arcos (en rojo) con ángulos α� y β� de dos circunferencias de radio R�: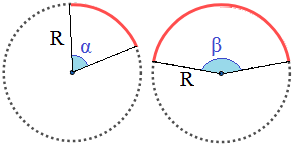
2. Fórmula de Longitud de ArcoPor el modo en el que hemos definido el arco (porción de una circunferencia), para calcular su longitud sólo tenemos que dividir la longitud de una circunferencia.La longitud de una circunferencia (o el perímetro de un círculo) es 2⋅π⋅R2⋅�⋅�, siendo R� su radio.Fórmula con el ángulo en grados:Como una circunferencia es un arco con ángulo 360∘360∘, la longitud de un arco con ángulo α∘�∘ en grados es
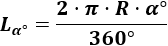Fórmula con el ángulo en radianesSi escribimos el ángulo β� en radianes, la fórmula es
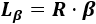X
3. Problemas ResueltosProblema 1Calcular la longitud del siguiente arco (radio R=3�=3 cm y ángulo α=126∘�=126∘):
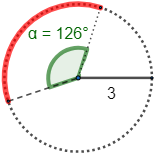Utilizamos la fórmula con el ángulo en grados: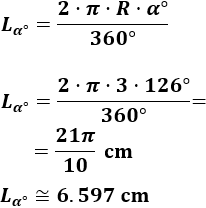
2. Fórmula de Longitud de ArcoPor el modo en el que hemos definido el arco (porción de una circunferencia), para calcular su longitud sólo tenemos que dividir la longitud de una circunferencia.La longitud de una circunferencia (o el perímetro de un círculo) es 2⋅π⋅R2⋅�⋅�, siendo R� su radio.Fórmula con el ángulo en grados:Como una circunferencia es un arco con ángulo 360∘360∘, la longitud de un arco con ángulo α∘�∘ en grados es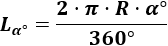Fórmula con el ángulo en radianesSi escribimos el ángulo β� en radianes, la fórmula es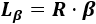X
3. Problemas ResueltosProblema 1Calcular la longitud del siguiente arco (radio R=3�=3 cm y ángulo α=126∘�=126∘):Utilizamos la fórmula con el ángulo en grados: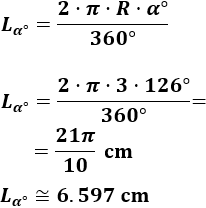Longitud de arco para funciones vectorialesHemos visto cómo una función de valor vectorial describe una curva en dos o tres dimensiones. Recuerde las fórmulas alternativas para la curvatura, que establece que la fórmula para la longitud del arco de una curva definida por las funciones paramétricas x = x (t), y = y (t), t1 ≤ t ≤ t2 viene dada por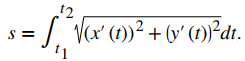
De manera similar, si definimos una curva suave usando una función de valor vectorial r (t) = f (t) i + g (t) j, donde a ≤ t ≤ b, la longitud del arco viene dada por la fórmula
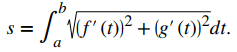En tres dimensiones, si la función de valor vectorial se describe por r (t) = f (t) i + g (t) j + h (t) k durante el mismo intervalo a ≤ t ≤ b, se da la longitud del arco por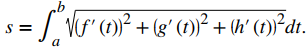
Las dos fórmulas son muy similares; solo difieren en el hecho de que una curva espacial tiene tres funciones componentes en lugar de dos. Tenga en cuenta que las fórmulas se definen para curvas suaves: curvas donde la función de valor vectorial r (t) es diferenciable con una derivada distinta de cero. La condición de suavidad garantiza que la curva no tenga cúspides (o esquinas) que puedan hacer que la fórmula sea problemática.EJEMPLO ILUSTRATIVO 10.10_1. Encontrar la longitud del arcoCalcule la longitud del arco para cada una de las siguientes funciones con valores vectoriales:
a. r (t) = (3t − 2) i + (4t + 5) j, 1 ≤ t ≤ 5
b. r(t) = ⟨tcost, tsent, 2t⟩, 0 ≤ t ≤ 2πSolución:a. Usando la primera ecuación del Teorema 10.10.1, r ′ (t) = 3i + 4j, entonces
b. Usando la segunda ecuación del Teorema 10.10.1, r ′ (t) = ⟨cost − tsent, sent + tcost, 2⟩, entonces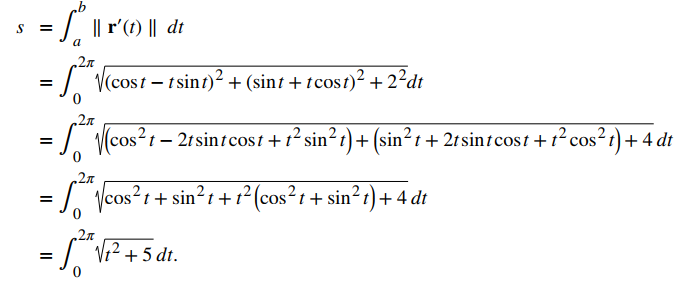
Aquí podemos usar una fórmula de integración de tablas
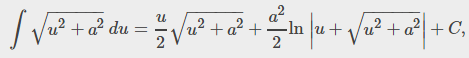entonces obtenemos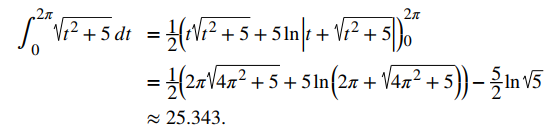
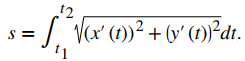De manera similar, si definimos una curva suave usando una función de valor vectorial r (t) = f (t) i + g (t) j, donde a ≤ t ≤ b, la longitud del arco viene dada por la fórmula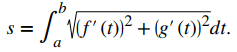En tres dimensiones, si la función de valor vectorial se describe por r (t) = f (t) i + g (t) j + h (t) k durante el mismo intervalo a ≤ t ≤ b, se da la longitud del arco por
TEOREMA 10.10.1 Fórmulas de longitud de arcoi. Curva plana: dada una curva suave C definida por la función r (t) = f (t) i + g (t) j, donde t se encuentra dentro del intervalo [a, b], la longitud del arco de C sobre el intervalo es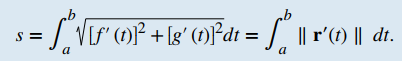 ii. Curva espacial: dada una curva suave C definida por la función r (t) = f (t) i + g (t) j + h (t) k, donde t se encuentra dentro del intervalo [a, b], la longitud del arco de C durante el intervalo es |
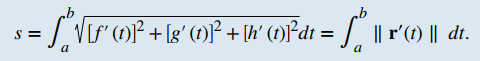b. Usando la segunda ecuación del Teorema 10.10.1, r ′ (t) = ⟨cost − tsent, sent + tcost, 2⟩, entonces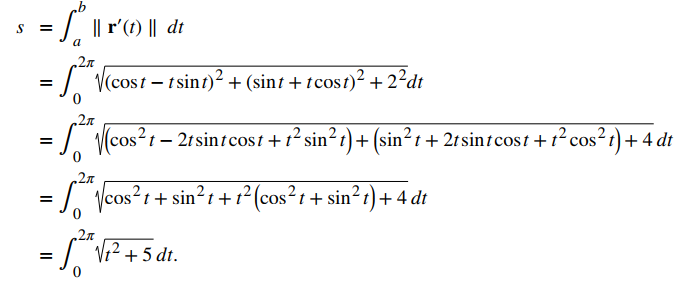Aquí podemos usar una fórmula de integración de tablas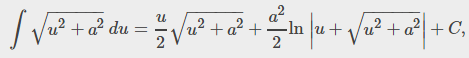entonces obtenemos