Elementary Row Operations and Echelon Form

Elementary Row Operations

Given a system of linear equations, we first express it as an augmented matrix. We work on the augmented matrix by performing a sequence of the so-called elementary row operations - the operations corresponding to how we manipulate the equations in the system during the variable-eliminating process. There are only three elementary row operations:

(Interchange) Interchange two rows (Notation: means interchange i^th and j^th row)
(Scaling) Multiply all entries in a row by a nonzero constant (Notation: means multiply i^th row by )
(Replacement) Replace one row by the sum of itself and a multiple of another row (Notation: means replace i^th row by the sum of i^th row and times j^th row)

Notice that these three elementary row operations are reversible -

can reverse

and

can reverse

. In fact, elementary row operations can be applied to any matrix, not just an augmented matrix. Two matrices are called row equivalent if there is a sequence of elementary row operations that transforms from one to another. The following is the important result that we will prove later in this chapter: Theorem: If the augmented matrices of two linear systems are row equivalent, then the two systems have the same set of solutions. Gaussian elimination is the procedure of transforming the augmented matrix of a linear system by a sequence of elementary row operations to the one in the so-called echelon form. And you will see that it is easy to obtain the solution(s) to the linear system with its augmented matrix in echelon form and hence solve the original linear system. You can try the "Row operation calculator" in "Linear Algebra Toolkit" developed by P. Bogacki.

Echelon Form

Given an augmented matrix of a system of linear equation, we say that a row in the matrix a nonzero row if at least one its entries is a nonzero entry. The leading entry is the leftmost nonzero entry (in a nonzero row). A matrix is in echelon form (or row echelon form) if it has the following three properties:

All nonzero rows are above any rows of all zeros.
Each leading entry of a row is in a column to the right of the leading entry of the row above it.
All entries in a column below a leading entry are zeros.

If a matrix in echelon form satisfies the following additional conditions, then it is in reduced echelon form (or reduced row echelon form):

The leading entry in each nonzero row is 1.
Each leading 1 is the only nonzero entry in its column.

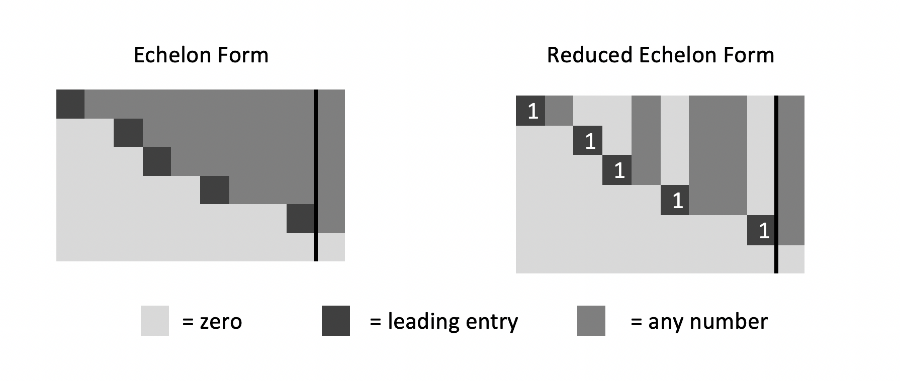
An augmented matrix may be row reduced (that is, transformed by a sequence of elementary row operations) to more than one matrix in echelon form. However, it can be shown that any matrix is certainly row reduced to a unique matrix in reduced echelon form. In each of the following questions, you need to determine whether an augmented matrix is in (reduced) echelon form or not:

The augmented matrix is

Select all that apply