Descent-ascent numerical method for finding the stationary points of a function of two variables without using its derivatives. 1.3
f₄(x, y) = kf*(x⁴ + y⁴ - 8x² - 18y² - 2)
*The applet will work at a much faster speed if you download it to a desktop computer.
The order of operations for computing stationary points can be found in the applet.
Interactively find and compute local extrema of a nonlinear function of two variables without using its derivatives.
Under the applet, you will find the stationary points of the function in question, calculated on a desktop computer, and you can compare them with more accurate calculations in CAS based on knowledge of the analytical formulas for its partial derivatives.
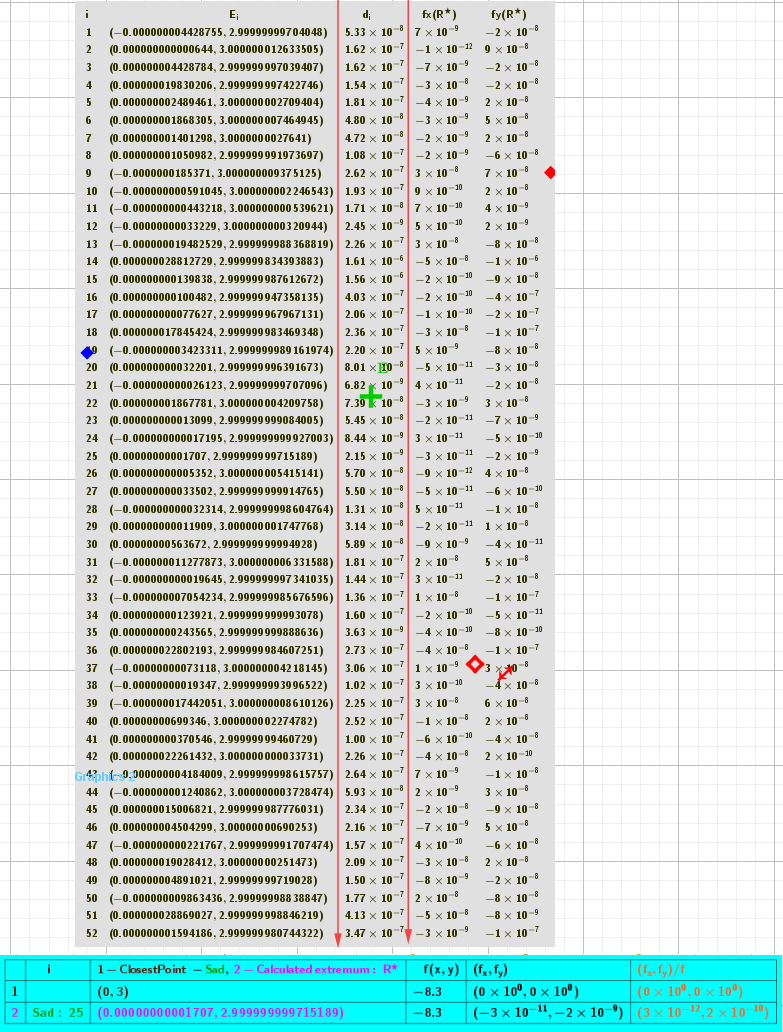
The iteration process consists of no+2 steps. When searching for local maxima and minima, the function values of the iteration points are sorted for all steps. However, such sorting is difficult because these values coincide within the accuracy of the GeoGebra algebra. Therefore, to find the largest/smallest value, this sorting is additionally performed in GeoGebra CAS with higher accuracy.
To calculate saddle points, di - the distance between two characteristic points for each iteration - was chosen as a criterion. The iteration is considered optimal if this distance is minimal. These distances for different iterations differ enough that the calculations can be done without using CAS.
*Explanations of the algorithms for searching for stationary points can be found in the applets 1 and 2.
Implicit curves of the equations: fx(x,y)=0 and fy(x,y)=0. Contour lines. Location of stationary points
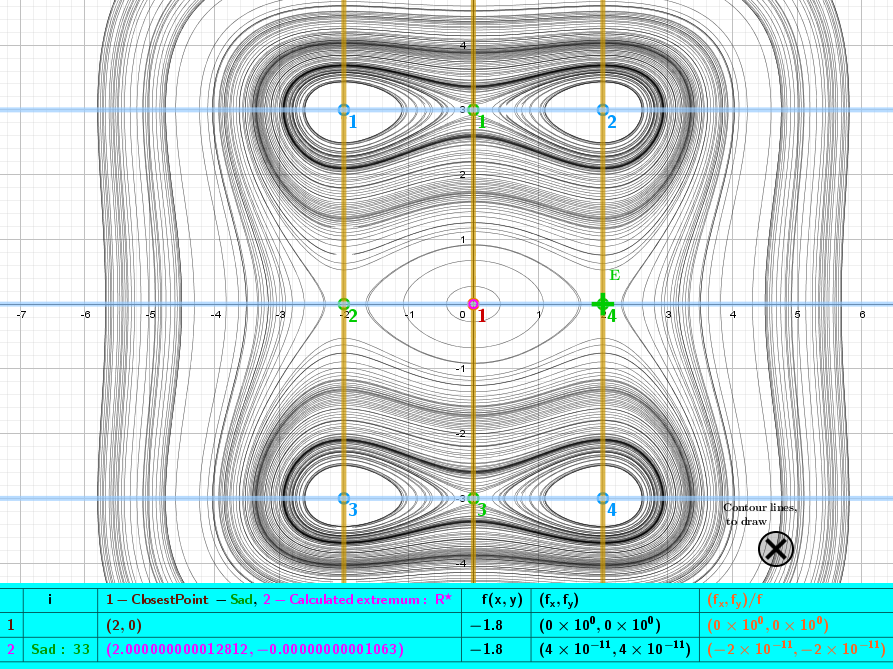
Calculated points of Local maxima

Calculated points of Local minima

Calculated Saddle Points

Case of iterative process of calculating minimum points

Case of iterative process of calculating saddle points