Découverte du théorème de Pythagore
1. Déplace les pièces de couleur des 2 plus petits carrés afin de les placer dans le plus grand. Les 5 pièces doivent couvrir la surface du plus grand carré. Tu peux faire pivoter les pièces à l'aide des points bleus.
Le théorème de Pythagore est un théorème de géométrie euclidienne qui met en relation les longueurs des côtés dans un triangle rectangle.
Ce théorème permet notamment de calculer l’une de ces longueurs à partir des deux autres. Il doit son nom à Pythagore de Samos, philosophe de la Grèce antique du vie siècle av. J.-C.
Plus généralement, ce théorème a de nombreuses applications dans divers domaines très différents (architecture, ingénierie...), encore aujourd'hui, et a permis nombres d'avancées technologiques à travers l'histoire.

Rappel :
- L'aire d'un carré de côté "a" est égale au carré de "a" , soit a2
- Dans un triangle rectangle : le côté opposé à l'angle droit est appelé hypoténuse , c'est le côté le plus long du triangle.
Exploitation du théorème
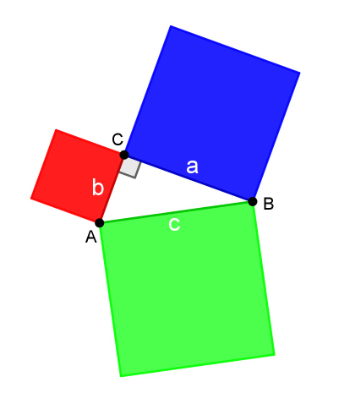
Dans la figure ci-dessous , ABC est un TRIANGLE RECTANGLE en C tel que :
le segment AB = c ;
le segment AC = b;
Le segment BC = a
Le carré bleu est un carré de côté a (BC).
Le carré rouge est un carré de côté b (AC).
Le carré vert est un carré de côté c (AB).
2. Écris l'expression de l'aire du carré bleu (expression littérale en fonction de la variable a). Tu dois te servir du clavier spécial () pour les exposants.
3. Ecris l'expression de l'aire du carré rouge (expression littérale en fonction de la variable b)
4. Ecris l'expression de l'aire du carré vert (expression littérale en fonction de la variable c)
5. Fais glisser les points colorés des petits carrés dans le grand carré.
6. Fais glisser le curseur vert vers la droite et le curseur bleu vers la gauche.
7. Que peux-tu dire des aires des trois carrés?
8. Écris une égalité qui comporte a2 , b2 et c2.
9. Dans cette partie, tu dois valider que a2+b2=c2
Déplace le point B de façon que le triangle ABC soit rectangle en B.
En faisant ce déplacement observe les calculs dans la partie encadrée en jaune.
Que remarques-tu?