Grenzuntersuchung (Fortsetzung)
Grenzverhalten berechnen
Theoretisch anspruchsvoller als das Rechnen mit Testeinsetzungen und das anschließende Beurteilen des Grenzverhaltes ist die Berechnung der Grenzwerte durch geschickte Termumformungen und Substitution.
Im Zählen und Nenner stehen Polynome. Ziel ist es, die Untersuchung durchzuführen, ohne dass das Nennerpolynom gegen Null oder Unendlich strebt.
Dazu wird die Untersuchung normiert und auf das Verhalten der Standard-Funktion zurückgeführt.
![Graph der Funktion [math]f:f\left(x\right)=\frac{1}{x}[/math]](https://www.geogebra.org/resource/sjxvnkmd/CAb47ksTGJOKipi5/material-sjxvnkmd.png)
- "Wenn x gegen plus oder minus Unendlich strebt, dann streben die Kehrwerte y=1/x gegen Null."
- "Wenn x von links gegen Null strebt, dann strebt y gegen minus Unendlich."
- "Wenn x von rechts gegen Null strebt, dann strebt y gegen plus Unendlich."
A: Verhalten im Unendlichen
Durch das vollständige Kürzen der höchsten Potenzen von x des Nennerpolynoms wird der Funktionsterm in in eine neue Form gebracht.
Dazu werden Zähler und Nenner durch Ausklammern von x faktorisiert und anschließend wird gekürzt.
Das wird solange gemacht, bis der Nenner im Grenzprozess gegen eine von Null verschiedene feste Zahl strebt.
Beispiel 1
Termumformung durch Kürzen:
Jetzt beurteilt man das Verhalten der einzelnen Teilterme für den betreffenden Grenzprozess .
Es ergibt sich: Wenn , dann .
Beispiel 2
Jetzt beurteilt man das Verhalten der einzelnen Teilterme für den betreffenden Grenzprozess .
Es ergibt sich: Wenn , dann .
B: Verhalten an einer Stelle
Durch eine geschickte Substitution wird der Funktionsterm in eine Form gebracht, in der sich sein Grenzverhalten für den zu untersuchende Grenzprozess leicht beurteilen läßt.
Die Standardsubstitution lautet mit .
Sie ersetzt den zu untersuchenden Grenzübergang durch den Übergang . Hier ist die Annäherung von links und von rechts an die Null zu durchdenken. Dabei hat h ein negatives oder positives Vorzeichen.
Problematisch ist der Fall, wenn das Nennerpolynom an der Untersuchungsstelle eine Nullstelle besitzt. Dann werden Zähler und Nenner durch Ausklammern von h faktorisiert und anschließend wird gekürzt. Das wird solange gemacht, bis der Nenner im Grenzprozess gegen eine von Null verschiedene feste Zahl strebt oder der Kehrwerte von h ohne Konflikt durch beurteilt werden kann.
Beispiel 1
Untersucht wird die Funktion an der Stelle .
Substitutuion und Termumformung:
Jetzt beurteilt man das Verhalten der einzelnen Teilterme für den betreffenden Grenzprozess .
Es ergibt sich:
Wenn , dann und , also .
Beispiel 2
Untersucht wird die Funktion an der Stelle .
Jetzt beurteilt man das Verhalten der einzelnen Teilterme für den betreffenden Grenzprozess .
Es ergibt sich:
Wenn , dann .
Graphen der Beispielfunktionen
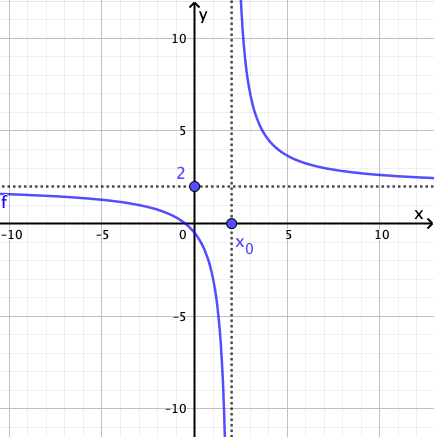
![Graph der Beispielfunktion [math]\text{f:f(x)=}\frac{2x^2+x}{x-2}[/math].](https://www.geogebra.org/resource/pvxjhgn6/wAVtn3mfh0B7swD1/material-pvxjhgn6.png)