Dokumentation: Satz des Pythagoras/ Goldener Schnitt
Im Folgenden werden mit den Themen "Satz des Pythagoras" sowie "Goldener Schnitt" zwei prominente Anwendungen von Ähnlichkeit vorgestellt. Während das Thema Ähnlichkeit im Bildungsplan einen größeren Umfang hat, werden hier nur die genannten Themen behandelt.
Satz des Pythagoras
Bildungsplan:
Der Satz des Pythagoras kommt im aktuellen Bildungsplan für Gymnasien in der Klassenstufe 7/8 unter der Leitidee Raum und Form vor. SuS sollen am Ende der Unterrichtseinheit zur Geometrie in der Lage sein, den Satz anzuwenden, um Streckenlängen zu errechnen. Gleichzeitig sollen sie den Kehrsatz kennen und mit dessen Hilfe von Streckenlängen eines Dreieckes auf Orthogonalität schließen können.
Ansonsten findet der Satz des Pythagoras in höheren Klassenstufen immer wieder Anwendungen (bspw. Länge eines Vektors), wird im Bildungsplan jedoch nicht erneut benannt.
Als Voraussetzungen wird explizit genannt, dass die SuS in der Lage sein sollen, einfache Formeln nach einer Variablen auflösen zu können. Dieses Wissen sollte in der Klassenstufe 7/8 unter der Leitidee Zahl - Variable - Operation behandelt werden. Da das Vorwissen in derselben Klassenstufe angesiedelt ist, wird der Satz des Pythagoras meistens erst in Klasse 8 behandelt.
Hinführung zum Thema:
Bevor der Satz des Pythagoras erstmals formalisiert aufgeschrieben wird (oder sogar bewiesen wird), empfiehlt es sich, auf den Satz und seine Korrektheit hinzuführen. Das Mathematikbuch Elemente der Mathematik 9 (Schroedel 2016) zeigt zuerst ein historisches Beispiel (siehe Abbildung unten), genauer das antike ägyptische Zwölfknotenseil. Hier kann ein rechter Winkel durch Strammziehen dreier Knoten gebildet werden. Diese Schnur kann mit GeoGebra oder sogar selbstgemacht mitgebracht werden, sodass die SuS diese Relation haptisch erfahren können.
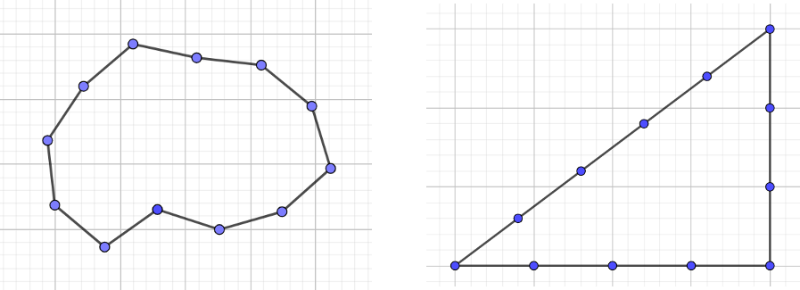
Diese Einführung eignet sich auch optimal als Stundeneinstieg, der Übergang zum rechnerischen Ausprobieren kann leicht gelingen.
Eine andere Option lässt die SuS auf ihr Vorwissen zu gleichschenkligen Dreiecken aufbauen. So enthält Elemente der Mathematik 9 eine Beispielaufgabe, in der die Dachsparren an einem Dachgiebel (dargestellt durch ein gleichschenkliges rechtwinkliges Dreieck) berechnet werden sollen. Hier lässt sich allein durch Umformen der bekannten Flächeninhaltsformel für gleichschenklige Dreiecke der Satz des Pythagoras für diesen Spezialfall zeigen. Auch dadurch können die SuS an die Vermutung herangeführt werden.
Satz des Pythagoras
Wenn ein Dreieck rechtwinklig ist, dann ist der Flächeninhalt des Hypotenusenquadrates gleich der Summe der Flächeninhalte der beiden Kathetenquadrate:
Für gilt, dass .
Beweisen
Eine der fünf prozessbezogenen Kompetenzen im Bildungsplan für Mathematik ist das mathematische Argumentieren und Beweisen. Daher bietet es sich an, den Satz des Pythagoras mithilfe von bekannten Sätzen, Definitionen und Axiomen zu beweisen.
Hierbei ist es nicht immer einfach, einen passenden Beweis oder eine passende Argumentation auszuwählen. Besonders der Satz des Pythagoras ist für seine Vielzahl von Beweisen bekannt, wodurch eine durchdachte Auswahl nötig ist (der Landesbildungsserver Baden-Württemberg verlinkt über 100 Beweise für den Satz des Pythagoras). Im Folgenden werden drei GeoGebra-Applets mit "Beweisen" gezeigt, wobei jeder einzelne davon seine Tücken und Probleme hat.
Schaufelradbeweis
Schopenhauers "Beweis"
Einsteins Beweis
Nutzen von Beweisen
Schnell stellt sich die Frage, welcher dieser Beweise den größten Nutzen im Schulunterricht hat.Der Schaufelradbeweis ist hier die wohl anschaulichste Art und Weise, um die Korrektheit des Satzes darzustellen. Mithilfe des GeoGebra-Applets lässt sich das Argument leicht in den Unterricht einbauen. Es würde außerdem bereits Aspekte von "Argumentieren und Beweisen" abdecken. Denn nicht nur das Kennen, Anwenden, Nachvollziehen und schließlich Beweisen eines Satzes (und seines Kehrsatzes) zählen zu dieser Kompetenz, sondern auch das begründete Äußern einer Vermutung oder das Finden von Gegenbeispielen. Für eine begründete Vermutung, dass der Satz des Pythagoras gelten muss, reicht der Schaufelradbeweis allemal.
Der Beweis Schopenhauers dagegen sollte nur mit Vorsicht gezeigt werden, da dieser nur einen Spezialfall zeigt. Hier könnte sogar fälschlicherweise bei SuS der Verdacht auf ein Gegenbeispiel naheliegen, was den Sinn des Beweisens im Unterricht konterkariert.
Der Beweis Einsteins ist dagegen eindeutig als mathematisch korrekter Beweis zu identifizieren. Das kann man unter anderem anhand von drei Kriterien (Weigand et al.) erkennen, die dieser Beweis alle erfüllt:
- Er ist lückenlos und vollständig (Voraussetzungen klar, alle Fälle abgedeckt, nur logische Schlüsse)
- Er ist minimal (keine redundanten Aussagen)
- Er ist formal (klar strukturiert, exakte Ausdrucksweise)
- Verifikation (Ist der Satz wahr?)
- Erklärung (Warum gilt der Satz?)
- Einordnung/ Systematisierung (Womit hängt der Satz zusammen?)
- Kommunikation (Wie formuliere ich die Aussage mathematisch genau?)
- Exploration/ Entdeckung (Welche Konsequenzen haben meine Annahmen/ Voraussetzungen? Welche weiteren Vermutungen lassen sich durch den Beweis entwickeln?)
Didaktische Analyse (Klafki)
Um die Frage zu beantworten, wie man als Lehrkraft ein Thema im Unterricht behandeln kann, lohnt es sich die Fragen der Didaktischen Analyse nach Klafki zu beantworten:
- Welchen allgemeinen Sinn- und Sachzusammenhang vertritt und erschließt dieser Inhalt?
- Welche Bedeutung hat dieser Inhalt bereits bei meinen Teilnehmenden?
- Welche Bedeutung hat dieser Inhalt für die Zukunft meiner Teilnehmenden?
- Welches ist die Struktur des Inhalts?
- Wie lässt sich dieser Inhalt am besten veranschaulichen? Wie kann dieser Inhalt interessant, fragwürdig, begreiflich gemacht werden?
Goldener Schnitt
Der Goldene Schnitt ist im Gegensatz zum obligatorischen Satz des Pythagoras ein optionales Thema, dass nicht im Bildungsplan der Mathematik vorhanden ist. SuS können ohne Weiteres ein Abitur in Baden-Württemberg machen, ohne jemals etwas vom Goldenen Schnitt oder von Fibonacci gehört zu haben.
Der Goldene Schnitt und die Fibonacci-Reihe kommt in vielen Bereichen des alltäglichen Lebens vor. Dabei sind nicht nur in Teilgebieten der Mathematik zu suchen. Denn auch in anderen Naturwissenschaften wie Chemie, Physik und Biologie, in der Informatik oder auch in musischen Bereichen wie Kunst, Design, Architektur oder sogar der Musik lassen sich Fibonacci-Zahlen oder das Verhältnis wiederfinden. Der Sachzusammenhang lässt sich an vielen Beispielen erkennen. Damit ist außerdem die Bedeutungsfrage für die Gegenwart und die Zukunft der SuS meist schnell geklärt.
Die Struktur dieses Zusatzthemas lässt sich nun sehr individuell gestalten. Während eine ähnliche Hinführung wie bei Pythagoras mit anschließendem Beweis (Errechnen des Verhältnisses, Konstruktion des Schnittes, Konstruktion einer Fibonacci-Spirale) durchaus sinnvoll sein kann, bietet ein Thema außerhalb des Bildungsplans mehr Freiheiten. So ist der Goldene Schnitt ein beliebtes GFS-Thema. Auch eine Kooperation mit anderen Fachrichtungen (z.B. Bildende Kunst) bietet sich an.
Anhand der zahllosen Beispiele aus den verschiedenen Gebieten (Blumen und Früchte, Moleküle, Bäume in der Natur, Bäume in der Informatik, Kunstwerke, Firmenlogos, Fotographie, berühmte Bauwerke,...) lässt sich der Goldene Schnitt schnell veranschaulichen. Dazu kann folgendes Applet dienen, bei dem die SuS enaktiv an einem ihnen vertrauten Bauwerk den Goldenen Schnitt entdecken können. Dazu benötigen aber alle SuS ein entsprechend geeignetes Gerät, für Smartphones ist dieses Applet unter anderem eher ungeeignet.
Goldener Schnitt am Karlsruher Schloss
Auf GeoGebra finden sich zahllose weitere Applets zum Thema. Auch Apps wie Pythagorea oder Euclidea können digitale Werkzeuge sein, um den Geometrieunterricht interessanter zu gestalten.
Die Frage nach anschaulicher Gestaltung kann aber auch ganz analog beantwortet werden, indem beispielsweise Maßbänder oder "Zirkel" mit dem Längenverhältnis des Goldenen Schnitts nachgemessen werden können. Auch das Konstruieren einer Fibonacci-Spirale auf Papier mit Lineal und Zirkel ist eine Möglichkeit, wie man dieses geometrische Thema greifbar machen kann.
Goldener-Schnitt-Zirkel

Fibonacci-Spirale
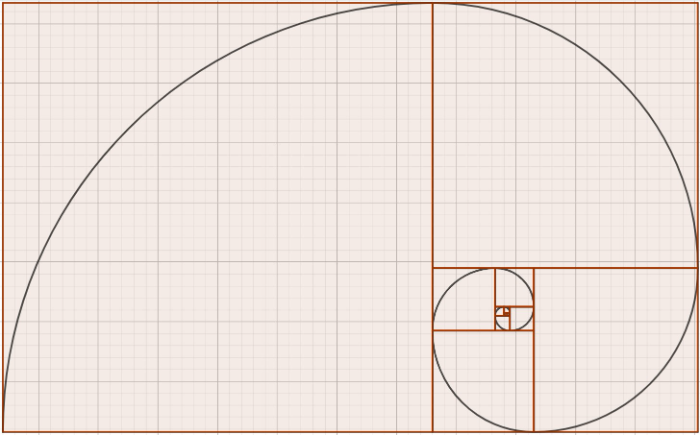
Fazit
Die beiden gezeigten Themen sind wie anfangs erwähnt Anwendungen der Ähnlichkeit. Anhand dieser beiden Themen, die im Bildungsplan nicht oder nur kurz eigenständig erwähnt sind, lassen sich verschiedenste Inhalte vermitteln. Das Vertiefen grundlegender mathematischer Kompetenzen wie das Beweisen ist genauso gut möglich und empfehlenswert wie das Vertiefen und Verknüpfen mit fächerübergreifendem Wissen.
Allgemein sollte die Anschaulichkeit und Anwendungsbezogenheit gerade im Geometrieunterricht nicht zu kurz kommen, da dieses ansonsten sehr formalisierte und abstrakte Teilgebiet der Mathematik sonst nur schwer für die SuS zugänglich werden kann.
