Виды многогранников
Многогранники можно выделить в следующие группы:
1. Правильные многогранники (Платоновы тела);
2. Выпуклые однородные многогранники - полуправильные многогранники (Архимедовы тела);
3. Звёздчатые формы и соединения;
4. Невыпуклые однородные многогранники (усечённые многогранники);
5. Призмы;
6. Пирамиды;
7. Многогранники, не входящие ни в одну из названных групп.
Платоновы тела. Платоновы многогранники
Именем Древнегреческого ученого - Платона названа группа из пяти геометрических тел. Пять многогранников, которые математики называют - правильные, мы чаще всего в обычной речи называем - Платоновы тела.
тетраэдр
октаэдр
куб
додекаэдр
икосаэдр
Почему эти пять геометрических тел, прежде всего, называют - правильные многогранники?
Это весьма легко запомнить. Стороны правильных многогранников являются правильными многоугольниками. А правильные многоугольники это те у которых, в свою очередь, равны все стороны (например: треугольник, квадрат) и равны углы между соседними сторонами. Причина возникновения слова правильные именно в этом.
Именем Древнегреческого ученого - Платона названа группа из пяти геометрических тел. Пять многогранников, которые математики называют - правильные, мы чаще всего в обычной речи называем - Платоновы тела.
тетраэдр
октаэдр
куб
додекаэдр
икосаэдр
Почему эти пять геометрических тел, прежде всего, называют - правильные многогранники?
Это весьма легко запомнить. Стороны правильных многогранников являются правильными многоугольниками. А правильные многоугольники это те у которых, в свою очередь, равны все стороны (например: треугольник, квадрат) и равны углы между соседними сторонами. Причина возникновения слова правильные именно в этом.
Многогранники Архимеда - 13 полуправильных многогранников
Древнегреческому ученому Архимеду принадлежит открытие 13 многогранников - "архимедовых тел", которые так же именуют полуправильными многогранниками. Каждое из них ограничено неодноименными правильными многоугольниками и в котором равны многогранные углы и одноименные многоугольники. Кроме того, в каждой вершине сходится одно и тоже число одинаковых граней. В одинаковом порядке каждое из этих тел может быть вписано в сферу.
Почему все архимедовы тела часто называют полуправильные многогранники?
Каждое из 13-ти Архимедовых тел является полуправильным многогранником по своим математическим свойствам. При этом надо помнить, что далеко не все полуправильные многогранники можно назвать архимедовыми, так как в группу полуправильных многогранников входит гораздо больше геометрических тел, а количество архимедовых многогранников очень мало - всего тринадцать. Впервые увидев эти 13 названий - "голова идет кругом". Всё смешивается. Однако запомнить и разобраться все-таки можно.
Как выглядит каждое из 13-ти Архимедовых тел?
1. Усечённый тетраэдр
2. Усечённый октаэдр
3. Усечённый куб (гексаэдр)
4. Усечённый додекаэдр
5. Усечённый икосаэдр
6. Кубо-октаэдр
7. Ромбо-кубо-октаэдр
8. Ромбо-усечённый кубо-октаэдр
9. Плосконосый куб (курносый куб)
10. Икосо-додекаэдр
11. Усечённый икосо-додекаэдр
12. Ромбо-усечённый икосо-додекаэдр
13. Плосконосый додекаэдр (другое название курносый додекаэдр)
Древнегреческому ученому Архимеду принадлежит открытие 13 многогранников - "архимедовых тел", которые так же именуют полуправильными многогранниками. Каждое из них ограничено неодноименными правильными многоугольниками и в котором равны многогранные углы и одноименные многоугольники. Кроме того, в каждой вершине сходится одно и тоже число одинаковых граней. В одинаковом порядке каждое из этих тел может быть вписано в сферу.
Почему все архимедовы тела часто называют полуправильные многогранники?
Каждое из 13-ти Архимедовых тел является полуправильным многогранником по своим математическим свойствам. При этом надо помнить, что далеко не все полуправильные многогранники можно назвать архимедовыми, так как в группу полуправильных многогранников входит гораздо больше геометрических тел, а количество архимедовых многогранников очень мало - всего тринадцать. Впервые увидев эти 13 названий - "голова идет кругом". Всё смешивается. Однако запомнить и разобраться все-таки можно.
Как выглядит каждое из 13-ти Архимедовых тел?
1. Усечённый тетраэдр
2. Усечённый октаэдр
3. Усечённый куб (гексаэдр)
4. Усечённый додекаэдр
5. Усечённый икосаэдр
6. Кубо-октаэдр
7. Ромбо-кубо-октаэдр
8. Ромбо-усечённый кубо-октаэдр
9. Плосконосый куб (курносый куб)
10. Икосо-додекаэдр
11. Усечённый икосо-додекаэдр
12. Ромбо-усечённый икосо-додекаэдр
13. Плосконосый додекаэдр (другое название курносый додекаэдр)
Звёздчатые формы и соединения
Кроме правильных и полуправильных многогранников красивые формы имеют так называемые звездчатые многогранники. Их всего четыре. Первые два были открыты Кеплером, а два других почти 200 лет спустя построил Пуансо (1777—1859). Они получаются из правильных многогранников продолжением их граней или ребер.
Из тетраэдра, куба и октаэдра звездчатые многогранники не получаются. Рассмотрим додекаэдр.
малый звездчатый додекаэдр
большой додекаэдр 
большой звездчатый додекаэдр 
большой додекаэдр
большой звездчатый додекаэдр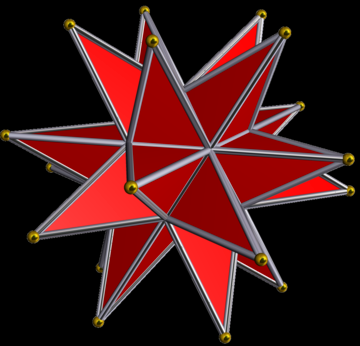
- большой икосаэдр
Правильные призмы
Призма - это многогранник, две грани которого, многоугольники по форме, являются основаниями, остальные грани (боковые грани) имеют форму параллелограмма.
Правильной призмой - является призма, у которой в основаниях правильные многоугольники, а боковые грани равные прямоугольники.
Высота призмы - это отрезок, перпендикулярный основаниям призмы.
В зависимости от числа углов основания, правильные призмы различают:
- треугольные или трехгранные призмы;
- четырехугольные или четырехгранные призмы;
и т.д.
Призма - это многогранник, две грани которого, многоугольники по форме, являются основаниями, остальные грани (боковые грани) имеют форму параллелограмма.
Правильной призмой - является призма, у которой в основаниях правильные многоугольники, а боковые грани равные прямоугольники.
Высота призмы - это отрезок, перпендикулярный основаниям призмы.
В зависимости от числа углов основания, правильные призмы различают:
- треугольные или трехгранные призмы;
- четырехугольные или четырехгранные призмы;
и т.д.
Правильные пирамиды
Пирамида - это многогранник, одна из граней которого является основанием, остальные грани это треугольники, имеющие общую вершину.
Правильной пирамидой - является пирамида, у которой в основании лежит правильный многоугольник и высота пирамиды проходит точно через его центр в основании.
Высота пирамиды - это перпендикулярный отрезок, проведенный через вершину пирамиды к плоскости её основания.
В зависимости от числа углов основания, правильные пирамиды различают:
- треугольные или трехгранные пирамиды;
- четырехугольные или четырехгранные пирамиды;
и т.д.
Пирамида - это многогранник, одна из граней которого является основанием, остальные грани это треугольники, имеющие общую вершину.
Правильной пирамидой - является пирамида, у которой в основании лежит правильный многоугольник и высота пирамиды проходит точно через его центр в основании.
Высота пирамиды - это перпендикулярный отрезок, проведенный через вершину пирамиды к плоскости её основания.
В зависимости от числа углов основания, правильные пирамиды различают:
- треугольные или трехгранные пирамиды;
- четырехугольные или четырехгранные пирамиды;
и т.д.