Desenhando Polígonos Estrelados
POLÍGONO REGULAR CÔNCAVO ESTRELADO“O estudo dos polígonos estrelados permite a exploração de fascinantes conexões entre a Teoria dos Números e a Geometria.”Se dividirmos uma circunferência em n partes iguais e ligarmos os pontos de divisão de p em p, andando sempre num mesmo sentido, terminaremos com o mesmo tipo de polígono que resulta da união dos pontos de n – p em n - p.
Passo de um polígono estrelado: É o número de divisões da circunferência que compreende uma corda (lado do polígono estrelado).
CLASSIFICAÇÃO DOS POLÍGONOSSeja n o número de vértices e p o número de lados do polígono inscrito em uma circunferência.Define-se:A) POLÍGONOS CONVEXOS: Ocorre quando MDC (n, p) = 1. Todos os vértices do polígono sobre a circunferência são unidos 1 a 1, em uma sequência definida.
B) POLÍGONOS ESTRELADOS: É quando para p ǂ 1, o MDC (n, p) = 1 e os pontos são unidos p a p, onde n e p são primos entre si.
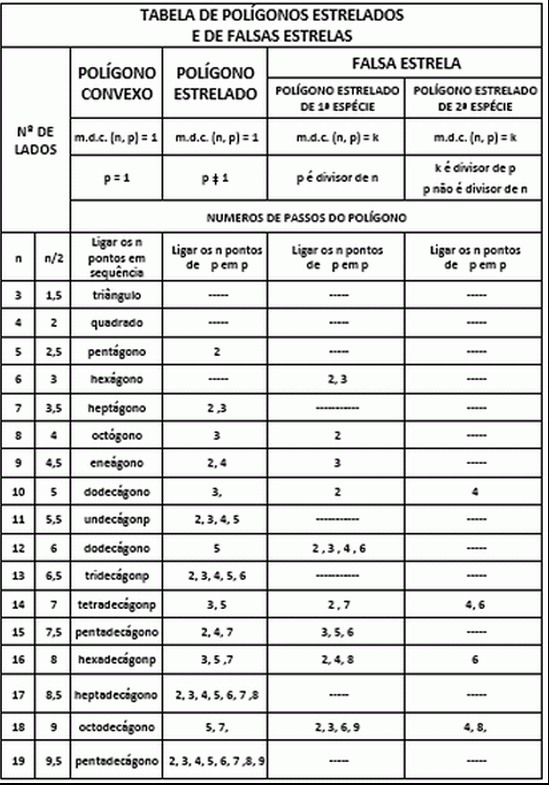
C) FALSA ESTRELAOcorre quando MDC (n, p) = K e k é divisor de n ou quando MDC (n, p) = K e k não é divisor de n
C-1) POLÍGONO ESTRELADO DE 1ª ORDEM:Ocorre quando MDC (n, p) = K e K é divisor de n. Exemplo n = 12 e p = 2 è MDC (12, 2) = 2 ǂ 1 è K = p = 2 é divisor de nPortanto, pode-se construir 2 hexágonos sobrepostos, o que caracteriza uma FALSA ESTRELA. Possui polígonos de n / p lados
C-2) POLÍGONO ESTRELADO DE 2ª ORDEM: Ocorre quando MDC (n, p) = K e K é não é divisor de n. Exemplo n = 14 e p = 4 logo MDC (14, 4) = 2 ǂ 1 è K = 2 é divisor de n e p não é
divisor de n. Possui polígonos de n / MDC (n, p) lados
Regra para a determinação do polígono regular côncavo estrelado.
Os polígonos regulares estrelados de n lados são os K polígonos onde p = (primocom n) < n/2.Para n par è nº de lados = n/2 - 1 Para n impar è nº de lados = parte inteira de (n/2)