BASE P3
Questão 1
As retas paralelas a e b representam espelhos planos, voltados
um para o outro. Construir a trajetória do raio luminoso que,
emitido de A, atinge B após refletir-se uma vez em a e uma vez
em b, respectivamente.
Questão 1
Um raio luminoso parte do ponto A e atinge o
ponto B após refletir-se sucessivamente nos
lados p, q e r do triângulo equilátero PQR.
Desenhe a trajetória do raio.
Questão 2
Nesta questão, o seu objetivos é determinar a reta s.
São dadas:
- a reta r;
- a reta t.
Sabe-se que:
- a reta t é transformada da reta r por homotetia com centro em S e razão −2/3;
- a reta s é transformada da reta r por homotetia com centro em S e razão 2/3.
Questão 2
Encontre r', a partir da reta r, dada.
Use a mesma homotetia negativa que associa os círculos (O,r) e (O', r') dados.
Considere o mesmo centro e a mesma razão de homotetia.
Questão 3
Nesta questão, os seus objetivos são:
- determinar os eixos e e f;
- desenhar o polígono A'B'C'D';
- desenhar o polígono A"B"C"D".
São dados:
- o ponto A'';
- o polígono ABCD;
- a reta r.
Sabe-se que:
- ;
- ;
- a reta r equidista dos eixos e e f;
- os eixos e e f são paralelos entre si.
Questão 3
Na noite de domingo, Luiz comprou uma pizza pelo iFood para dividir com seus 3 irmãos, Pedro, Frederico e Otávio. Desde o início, ficou combinado o seguinte: Pedro faria o primeiro corte e Frederico seria responsável pelo segundo, ambos em linha reta. Se porventura houvesse diferença na área de cada fatia, Luiz teria o direito de escolher o maior pedaço. Dito e feito. Pedro começou bem, dividindo a pizza pela metade com precisão nanométrica. Depois foi a vez de Frederico. Veja, ele até começou do ponto certo mas logo tomou a direção errada. A linha de corte de Frederico partiu do ponto A pertencente à borda da pizza, cruzou com a linha divisória de Pedro no ponto B e acabou terminando no ponto C. Sabendo que AB/BC = 4/3, determine as posições dos pontos A, B e C.
Questão 4
Construa o triângulo ABC.
São dados:
- a mediatriz m de AC;
- a mediatriz n de BC;
- o ponto médio M do lado AB.
Questão 4
Construa o triângulo ABC.
São dados:
- a mediatriz m de AC;
- a bissetriz s do ângulo interno do vértice C;
- o ponto médio M do lado AB.
Questão 5
Nesta questão, os seus objetivos são:
- determinar os pontos E e F;
- construir o caminho poligonal AEFC.
Apenas o triângulo ABC é dado.
Sabe-se que:
- o ponto E pertence ao segmento AC;
- o ponto F pertence ao segmento BC;
- os segmentos AE, EF e FC são congruentes.
Questão 5
Nesta questão, os seus objetivos são:
- determinar os pontos E e F;
- construir o caminho poligonal AEFC.
Apenas o triângulo ABC é dado.
Sabe-se que:
- o ponto E pertence ao segmento AC;
- o ponto F pertence ao segmento BC;
- os segmentos AE, EF e FC são congruentes.
Questão 6
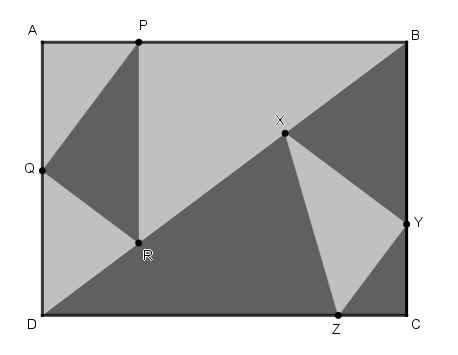
Um artista desenhou um retângulo com lados adjacentes em razão 4 para 3. Depois ele o dividiu por uma de suas diagonais em duas partes congruentes. Mais adiante ele produziu dois triângulos (PQR e XYZ) semelhantes aos que apareceram após a divisão inicial (BAD e DCB). Considere que:
- o triângulo PQR está inscrito no triângulo BAD;
- o triângulo XYZ está inscrito no triângulo DCB;
- o segmento PR é paralelo ao segmento BC;
- o segmento XY é paralelo à diagonal AC do retângulo ABCD.
Questão 6
Junte as três peças dadas, sem sobreposição, e forme uma figura composta simétrica por reflexão.
Ao terminar, construa o eixo de reflexão (de cor vermelha) usando a ferramenta de mediatriz.
- Clique e arraste o ponto preto para transladar a peça correspondente.
- Clique e arraste o ponto vermelho para rotacionar a peça correspondente.
- Clique no ponto azul para refletir a peça corresponde.